| |
|
|
|
| |
|
|
| |
DESCRIPCION DE LOS MOVIMIENTOS DE UN FLUIDO |
|
| |
|
|
| |
Para describir los movimientos de un fluido se usa generalmente la descripción de campo o Euleriana, la cual se basa en el estudio de las propiedades del flujo que pasa por un determinado lugar, tal como la velocidad (V), aceleración (ā), dirección, presión, densidad etc. El lugar en cuestión puede ser un simple punto o un espacio más amplio, si se quiere hacer un estudio de campo del flujo que lo atraviesa.
|
|
| |
|
|
| |
En esta descripción del movimiento de los fluidos, las propiedades del flujo son funciones del espacio y del tiempo. |
|
| |
|
|
| |
Tomemos por ejemplo la velocidad, esta se puede expresar en coordenadas cartesianas como: |
|
| |
|
|
| |
donde la región de flujo considerada se llama campo de flujo. |
|
| |
|
|
| |
CLASIFICACIÓN DE LOS FLUJOS |
|
| |
|
|
| |
Según la variación del flujo en el tiempo |
|
| |
Si el flujo es variable en el tiempo se dirá que este es transitorio o no estacionario.
En cambio cuando este no varía con el tiempo se dirá que este es estable o estacionario. |
|
| |
|
|
| |
En este último caso las variables del flujo dependen solo de las coordenadas espaciales, por ejemplo la velocidad sería: |
|
| |
|
|
| |
Lo cual nos indica que los cambios respecto al tiempo son nulos: ∂V / ∂t = 0. Y esto para todas las propiedades del flujo. La figura muestra un ejemplo de un flujo no estacionario en un canal abierto. |
|
| |
|
|
| |
Según la variación del flujo en el espacio |
|
| |
Cuando no existe cambio de las propiedades en el espacio se dirá que el flujo es uniforme, y en caso contrario el flujo será no uniforme. |
|
| |
|
|
| |
En el caso del flujo uniforme las variables del flujo dependen solo de las coordenadas temporales, por ejemplo la velocidad se expresará como |
|
| |
|
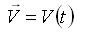 |
|
| |
lo cual indica que las variaciones en el espacio son cero: ∂V / ∂x = ∂V / ∂y = ∂V / ∂z = 0. |
|
| |
|
|
| |
En los casos reales es difícil conseguir flujos estrictamente uniformes, sin embargo en muchos casos prácticos de la mecánica de fluidos se pueden simplificar los fenómenos considerando que el flujo es uniforme.
|
|
| |
|
|
| |
En la figura siguiente se muestra un ejemplo de flujo en un canal abierto, en donde el flujo puede considerarse como uniforme o como no uniforme según el comportamiento que presenta. |
|
| |
|
|
| |
|
|
| |
|
|
| |
Según el número de variables espaciales a considerar |
|
| |
En esta parte podemos clasificar el flujo como unidimensional, bidimensional o tridimensional.
En la descripción Euleriana el flujo es por defecto tridimensional, ya que depende de tres variables espaciales, en coordenadas cartesianas x, y, z.
|
|
| |
|
|
| |
Sin embargo en muchos casos prácticos es posible simplificar la representación del flujo y considerar solo dos componentes espaciales (x, y o x, z) en cuyo caso el flujo se denominará bidimensional. Esto se puede hacer cuando las propiedades (o propiedad en estudio) del flujo cambian preponderantemente en solo dos direcciones, siendo practicante constante en la otra. Por ejemplo en el caso de un flujo plano en donde el vector velocidad depende de solo dos coordenadas espaciales. |
|
| |
|
|
| |
En muchos casos es incluso posible el considerar solo una componente espacial para estudiar el flujo (x), en cuyo caso éste se denominará unidimensional. Esto es el caso del flujo en una tubería, en donde el vector velocidad se puede representar con una sola componente espacial. |
|
| |
|
|
| |
Líneas de trayectoria, líneas de traza y líneas de corriente. |
|
| |
|
|
| |
Para ayudarnos en la descripción del comportamiento del movimiento de un fluido se pueden utilizar diversas herramientas como lo son las líneas de flujo, de las cuales podemos mencionar tres tipos. |
|
| |
|
|
| |
Línea de trayectoria |
|
| |
Es el lugar geométrico de los puntos recorridos por una partícula que viaja en el campo de flujo.
|
|
| |
|
|
| |
La figura muestra un ejemplo de líneas de trayectoria de partículas debajo de una ola en un tanque de agua. |
|
| |
|
|
| |
Línea de traza |
|
| |
Una línea de traza se define como una línea instantánea cuyos puntos están ocupados por todas las partículas que se originan un punto específico del campo de flujo.
|
|
| |
|
|
| |
La figura muestra el ejemplo de traza para un flujo inestable alrededor de un cilindro. |
|
| |
|
|
| |
Línea de corriente |
|
| |
Es una línea de flujo en donde el vector velocidad de cada partícula que ocupa un punto en la línea de corriente es tangente a dicha línea de corriente, tal como se muestra en la figura. |
|
| |
|
|
| |
La línea de corriente se puede expresar matemáticamente con la siguiente ecuación: |
|
| |
|
|
| |
Donde V y dr son los vectores de velocidad y cambio de posición, los cuales al ser paralelos su producto vectorial es cero. |
|
| |
|
|
| |
Tubo de corriente |
|
| |
Es un tubo cuyas paredes están formadas por líneas de corriente. Esto representa un tubo de donde las partículas no pueden salir ya que la velocidad en las paredes es paralela a ellas.
|
|
| |
|
|
| |
La noción del tubo de corriente tiene un particular interés en mecánica de fluidos ya que con el se pueden representar casos prácticos, como por ejemplo el flujo en una tubería, de la cual no pueden salir el flujo, por lo tanto se puede considerar como un tubo de corriente. |
|
| |
|
|
| |
En un flujo estacionario, las líneas de trayectoria, de traza y de corriente coinciden. Esto ya que todas las partículas que pasan por un punto dado van a describir la misma trayectoria, y la velocidad en la línea formada tiene siempre una dirección paralela a esta. |
|
| |
|
|
| |
|
|
| |
|
|
|
| |
|
|
| |
|
|
