UNIVERSIDAD DE LOS ANDES FACULTAD DE INGENIERÍA POSTGRADO EN COMPUTACIÓN

---

Tema 2. Modelos de objetos

Prof. Isabel Besembel Carrera

Núcleo La Hechicera. Edif. Economía. 3er. piso. Ala 3S. Mérida. Venezuela.

Sesión 3. Modelos físicos. Tabla de contenido:

Definición de una BD en un modelo genérico Relaciones de soporte de acceso Definiciones Estructura de almacenamiento Índices sobre la jerarquía de tipos	La función de materialización Representación de almacenamiento para las RGM Ubicación de los objetos Descomposición y replicación Otros modelos de almacenamiento físico
Referencia bibliográfica: Kim, W. Modern database systems. The object model, interoperability, and beyond. Addison Wesley / ACM Press. Capítulo 9. 1995.	Referencia bibliográfica: Willshire, M. y Kim, H. Properties of Physical Storage Models for Object-Oriented Databases. IEEE PARBASE-90. 1990.

Programa del curso

Definición de una BD en un modelo genérico de objetos (Generic Object Model)

Ejemplos de consultas:

Un ejemplo de extensiones se puede ver en la figura 1.

Figura 1. Ejemplo de extensiones de la base de datos anterior.

Relaciones de soporte de acceso (RSA):

Indización de expresiones de caminos:

• El producto por igualdad de valores de los atributos tiene un rol menos dominante en BDOO. El acceso por cadenas de referencias es más importante (join implícitos).
• Las relaciones de soporte de acceso constituyen materializaciones de las cadenas de referencia más utilizadas.

Definiciones:

• Una expresión de camino es o.A₁. ... .A_n donde o es un objeto cuya estructura es una tupla que contiene el atributo A₁, y o.A₁. ... .A_i refieren a un objeto o a un conjunto de objetos donde todos ellos tienen un atributo A_i+1.
• El resultado de una expresión de camino es un conjunto de objetos o valores del tipo T_n que puede ser alcanzado desde o a través de la cadena de atributos especificada.
• Expresión de camino: Sean t₀,...,t_n tipos no necesariamente distintos. Una expresión de camino sobre t₀ es una expresión t₀.A₁. ... .A_n si para cada 1 < = i < = n una de las dos condiciones se cumple:

• Relaciones de soporte de acceso: Sean t₀,...,t_n tipos y t₀.A₁. ... .A_n una expresión de camino. Una relación de soporte de acceso [t₀.A₁. ... .A_n] es de aridad n+1 y sus tuplas tienen la forma [S₀,...,S_n]
• El dominio del atributo S_i es el conjunto de oids de los objetos de tipo ti con 1 <= i <= n.

• Relaciones binarias temporales: Para cada atributo en la expresión de camino se tiene una relación binaria temporal [t_i-1.A_i], que contiene las tuplas (oid(O_i-1), oid(O_i)) para cada objeto O_i-1 de tipo t_i-1 y O_i de tipo t_i tal que:

• Extensiones de las relaciones de soporte de acceso:

Aplicabilidad: Una RSA [t₀.A₁. ... .A_n] _X bajo la extensión X es aplicable en el camino s.A_i. ... .A_j, donde s es un subtipo de t_i-1 bajo las condiciones siguientes:

La extension completa puede ser utilizada para evaluar cualquier subcamino, las izquierda y derecha pueden utilizarse solamente para evaluar prefijos y sufijos de caminos, respectivamente, y la canónica solo para evaluar un camino completo.

Estructura de almacenamiento

La estructura de almacenamiento para las RSA está basada en la propuesta de Valduriez 1987 denominada índice de producto binario. Cada RSA se almacena en dos índices, el primero tiene como clave el atributo más a la izquierda y el segundo el atributo más a la derecha. La estructura de los índices pueden ser: tablas hash o árboles_B+. La figura 3 muestra una ilustración de ello.

Figura 3. Uso de índices de acceso con árboles_B+.

El árbol_B+ de la izquierda agrupa hacia adelante y el de la derecha agrupa hacia atrás. El recorrido hacia atrás constituye un semi-producto derecha-a-izquierda:

El recorrido hacia adelante se corresponde con un semi-producto izquiera-a-derecha:

El índice de caminos de Maier y Stein 1986 se restringe a caminos que contengan atributos monovaluados y su representación está limitada a particiones binarias. Los usados en Orion son un caso especial de las RSA.

Índices sobre la jerarquía de tipos

• Los índices pueden verse como un caso especial de las RSA.
• Un índice por tipo: Cada tipo tiene un índice por el atributo especificado. La figura 4 muestra un ejemplo de este caso.

Figura 4. Ejemplo de índice por tipo.

• Índice sobre la jerarquía de tipos: Consiste de un árbol_B+ que contiene todas las instancias directas o indirectas del tipo indexado. Kim, Kim y Dale 1989 modificaron la estructura de las hojas para contener los desplazamientos para encontrar los Oids de cada tipo, de la forma mostrada en la figura 5.

Low,Ooi y Lu 1992 proponen los árboles_H que son construidos anidando los árboles_B+, así el índice de un subtipo está dentro del índice del supertipo. La figura 6 ilustra un ejemplo de estos.

Figura 6. Ejemplo de árboles_H.

El rango de un subárbol referenciado por un apuntador L debe estar contenido en el rango del árbol del supertipo. Todos los nodos hojas del árbol del subtipo son cubiertos por el árbol del subtipo.

La función de materialización

• Se modifican y recompilan solamente las clases (tipos) cuyas instancias están involucradas en alguna materialización.
• Relación generalizada de materialización (RGM): Sea t₁, ..., t_n, t_{n + 1}, ... t_{n + m} unos tipos y f₁, ..., f_n unas funciones no transformadoras con f_j: t₁, ..., t_n -> t_{n + j}, para 1 < = j < = m.

• Una RGM < f₁, ... , f_m > es consistente si su indicador de validez es verdadero.

• Si hay una actualización de la BD que invalida un resultado de una función de materialización se puede realizar una:

Ejemplo: para Q2

< Empleado . competencia >

La RGM < Empleado . competencia > contiene una competencia válida para todas las instancias de Empleado.

Representación de almacenamiento para las RGM

• El mejor soporte de acceso para las RGM es un índice multidimensional sobre los campos O₁, ... O_n, f₁, ..., f_m. Son n + m columnas que constituyen las n + m claves del índice (n + m) - dimensional. Los m bits de validez V₁, ..., V_m son atributos adicionales almacenados en el índice. La estructura archivo malla de Nievergelt et al. 1984 no arroja rendimientos favorables para más de 4 dimensiones.

• Invalidación y rematerialización de los resultados de las funciones: En la mayoría de los modelos las referencias a otros objetos son unidireccionales. La relación de referencia inversa (RRI) es usada por el manejador de RGMs para mantener los objetos relacionados con la materialización.

• Relación de referencia inversa: Es un conjunto de tuplas de la forma

Las referencias inversas se insertan en la RRI durante los procesos de materialización. Durante una rematerialización las modificaciones de las funciones son invocadas. Cada vez que un objeto es actualizado en la base de objetos, la RRI se inspecciona para determinar cual resultado materializado tiene resultados inválidos.

• Estrategias para reducir el overhead por invalidación:

1. Aislamiento de las propiedades relevantes del objeto: Normalmente los resultados materializados no dependen sino de una fracción del estado de los objetos visitados en la materialización. Ejm: la competencia no depende del sexo del Empleado.
2. Reducción de los chequeos de la RRI: Mantener más información dentro de los objetos para evitar mirar la RRI para todos los objetos actualizados.
3. Explotar la encapsulación estricta: Un subobjeto no puede ser actualizado separadamente de su objeto, por lo que se puede reducir el número de invalidaciones con el disparo de la invalidación del objeto de alto nivel.
4. Compensación de las actualizaciones: En vez de usar la función de materialización para recalcular un resultado inválido, se pueden usar acciones compensatorias que usen el resultado viejo y los parámetros de la actualización para recalcular el nuevo resultado de forma más eficiente.

Ubicación de los objetos

• El agrupamiento (clustering) es la colocación de objetos relacionados lógicamente en áreas físicas contiguas. Su efectividad se mide por el número de faltas de página que ocurren durante una aplicación. Enfoques: agrupamiento basado en la secuencia y agrupamiento basado en la partición.
• Agrupamiento basado en la secuencia: Agrupa los objetos en una secuencia específica en disco. Fases: preordenamiento y recorrido. En la primera todos los objetos son ordenados y en la segunda, los objetos ordenados sirven de raíz para el algoritmo de recorrido. Todos los objetos alcanzables desde el objeto raíz son anexados a la secuencia de agrupamiento en disco de acuerdo a su orden de visita. Si una secuencia es muy larga y no cabe en una página, se comienza una nueva secuencia cuya raíz es el objeto donde se quedó. Cuidar el almacenamiento doble.

El orden puede ser en base al tiempo de creación del objeto o a uno especificado por el usuario. Los algoritmos de recorrido son: primero-en-profundidad, primero-a-lo-ancho y primero-el-mejor.

En primero-el-mejor las referencias tienen un peso. Si se usa 0 y 1 como pesos, el algortimo puede ser especificado por un árbol de ubicación. La figura 7 presenta un ejemplo.

Figura 7. Ejemplo de un árbol de ubicación.

• Agrupamiento basado en la partición: Particionar un grafo en subgrafos disjuntos. Basándose en los pesos de las referencias, se tienen dos algoritmos:

• Posibilidades de ubicación de los objetos:

Descomposición y replicación

• Modelo de almacenamiento N-ario (MAN): Los objetos se consideran tuplas N-arias que comprenden todos los atributos expresados en su estructura, incluso los heredados. Se pueden almacenar en un único archivo, pero eso viola el agrupamiento.
• Modelo por descomposición (MAD): Cada valor de atributo se almacena separadamente, (Oid, atributo, valor) donde valor es un valor átomico o un Oid. Considerada deficiente para aplicaciones no distribuidas.
• Modelo híbrido (MADP): Los objetos se fragmentan verticalmente en base a la afinidad de sus atributos (los que siempre se usan en conjunto). Cuando un atributo debe usarse en más de un fragmento, se replica. Una fragmentación natural se obtiene de la jerarquía subtipo/supertipo. Ejemplo:

Otros modelos de almacenamiento físico

Se presentan otros modelos de almacenamiento físico según Willshire y Kim en [WiK-90]. Para ello se utilizará la base de datos ejemplo mostrada en la figura 8.

Figura 8. Estructura lógica de la base de datos de ejemplo.

1.- Modelo físico 1:

• Cada instancia está una sola vez en la BD, en la clase más específica. Ejm: Orion.
• Espacio: No hay duplicación de datos. Costos de espacio mínimo.
• Recuperación de una instancia: Al ser localizada la instancia no hay necesidad de buscar en otra parte.
• Modificación de un valor en una instancia: Solo se modifica la instancia escogida.
• Inserción de una nueva instancia: Solo afecta a una clase.
• Eliminación de una instancia: Solo involucra a dicha instancia, si no hay composición.
• Evolución del esquema: La creación de una nueva clase puede afectar el almacenamiento, si existen instancias viejas que deban migrar para mantener el modelo.
• Indexación: Se prefiere un índice por la jerarquía de clases.

La figura 9 ilustra el almacenamiento de las instancias en el modelo físico 1.

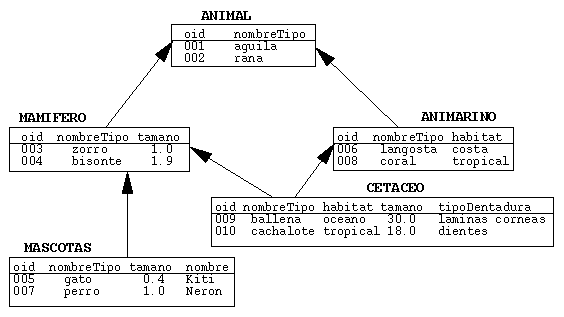
Figura 9. Modelo físico 1.

2.- Modelo físico 2:

• Cada instancia está en cada clase que la utilice.
• Espacio: Duplicación excesiva de datos. Costos de espacio máximo.
• Recuperación de una instancia: Al ser localizada la instancia no hay necesidad de buscar en otra parte. Preguntas sobre todas las instancias de una clase se responden sin ir a otro sitio.
• Modificación de un valor en una instancia: Múltiples modificaciones.
• Inserción de una nueva instancia: Múltiples escrituras de los datos.
• Eliminación de una instancia: Múltiples eliminaciones y escrituras.
• Evolución del esquema: La creación de una nueva clase implica escribir datos hacia arriba en la jerarquía. Si se elimina una, implica múltiples eliminaciones.
• Indexación: Se prefiere un índice por clase.

La figura 8 ilustra el almacenamiento de las instancias en este modelo.

3.- Modelo físico 3:

• Cada instancia almacena el oid y los atributos que le competen. Ejm: Iris.
• Espacio: Duplicación del oid de los datos. Costos de espacio buenos.
• Recuperación de una instancia: Involucra productos de extensiones de clases por el oid de los objetos.
• Modificación de un valor en una instancia: Hay que acceder la raíz para conocer oid y luego ubicar al atributo en la clase donde se escribirá.
• Inserción de una nueva instancia: Múltiples escrituras en las clases adecuadas.
• Eliminación de una instancia: Todas las instancias con igual oid son eliminadas.
• Evolución del esquema: La creación de una nueva clase no afecta sino a la jerarquía, donde hay que enlazar la nueva clase. Eliminación de una clase involucra varias modificaciones en las clases existentes que usen los oids.
• Indexación: No necesita un índice por la jerarquía de clases.

La figura 10 presenta el posicionamiento de las instancias para este modelo.

Figura 10. Ejemplo correspondiente al modelo 3.

4.- Modelo físico 4:

• No soporta la noción de clase y ella debe ser deducida por el patrón de nulos.
• Espacio: Inclusión de un valor nulo. Costos de espacio grande.
• Recuperación de una instancia: Solo se localiza la instancia.
• Modificación de un valor en una instancia: Solo se modifica una instancia.
• Inserción de una nueva instancia: Se anexa una nueva fila a la tabla.
• Eliminación de una instancia: Se elimina una fila de la tabla.
• Evolución del esquema: La creación/eliminación de clases se hace igual que las instancias. Se anexan/eliminan columnas a la tabla.
• Indexación: Se prefiere un índice por jerarquía de clases.

5.- Modelo físico 5:

• Variación del anterior, pero eliminando el uso de valores nulos. Oids se forman con el identificador de la clase más específica y su número de instancia. Ejm: Taxis.
• Espacio: Simple relación sin excesivo almacenamiento.
• Recuperación de una instancia: Se recupera el Oid y su valor.
• Modificación de un valor en una instancia: Solo se modifica una instancia.
• Inserción de una nueva instancia: Se anexa nuevas filas a la tabla.
• Eliminación de una instancia: Se elimina las filas relacionadas de la tabla.
• Evolución del esquema: La creación/eliminación de clases hace que sus Oids se creen o eliminen . Se anexan/eliminan filas a las tablas.
• Indexación: Se prefiere un índice por jerarquía de clases.

Programa