Recursivamente regresando al inicio Aleph-w: Algoritmos y estructuras de datos

Principios generales

Principios generales de diseño y programación

El diseño de $\aleph_\omega$ Aleph-w está orientado hacia grupos de clases de objeto según su granularidad en lugar de capas según su funcionalidad.

En este contexto, la granularidad de una clase es una idea que da cuenta de su complejidad bajo las siguientes consideraciones:

  1. La continuidad de memoria: una clase cuya estructuración en memoria sea contigua, básicamente que no contenga punteros a zonas discontinuas, y que represente a una sola unidad se considera de granularidad baja o fina. Por ejemplo, los tipos básicos del compilador (int, float, etc) son tipos de granularidad muy fina. También, objetos simplemente estructurados, tales como números complejos, y otros de $\aleph_\omega$ Aleph-w como Point, Slink, Dlink, etc. son de granularidad fina.
  2. Funcionalidad mínima por herencia: funcionalmente hablando, una clase es de baja granularidad en la medida en que sus métodos sean indispensables a su nivel de herencia de clases. En ese sentido, un método dado debe exportarse desde el nivel de clase más bajo.

La siguiente figura esquematiza un panorama arquitectural de $\aleph_\omega$ Aleph-w:

capas.png

Note que estos grupos no necesariamente se corresponden con los módulos planteados en este manual. Se trata de grupos de diseño según la granularidad.

Fundamentalmente, según la granularidad, $\aleph_\omega$ Aleph-w se compone de cinco (5) grandes grupos de clases:

  1. Clases de granularidad fina.
  2. Clases de granularidad intermedia.
  3. Clases de representación.
  4. Contenedores
  5. Algoritmos.

Clases de granularidad fina

Las clases de grano fino son bastante incompletas en el sentido de que no están diseñadas para utilizarse por si solas, sino como parte de una estructura de datos.

A esta categoría pertenecen las clases Slink, Dlink, Point y Segment.

De este grupo, quizá la más notoria, por su empleo prácticamente ubicuo en el resto de la biblioteca, es la clase Dlink, la cual representa un doble enlace de una lista circular, doblemente enlazada, con nodo cabecera. Dlink en si no tiene sentido sin pensar en otra estructura de dato, pero separarla tiene grandes ventajas, entre la cuales se puede señalar:

Muy parecido ocurre con la clase Point y otras clase y algoritmos de la geometría computacional.

Clases de granularidad intermedia

Todas las clases que pertenecen a este grupo son "nodos" de listas enlazadas, de árboles, de tablas hash y de grafos y de redes de flujo. Adicionalmente, también hay "arcos" de grafos y redes.

A este grupo pertenecen las clases Dnode, Snode, BinNode, AvlNode, RbNode, Rand_Node, TreapNode, BinHeapNode, Graph_Node, Arc_Node, Net_Node y Net_Arc.

Cada nodo tiene un tipo de dato asociado.

En este nivel, tampoco tiene mucho sentido el uso aislado, pero si existe un uso de especificación. Hay dos formas de especificación:

  1. Definición de un componente de una estructura de dato posterior: por ejemplos, para usar árboles splay se debe definir el nodo de un árbol splay, el cual es de tipo BinNode y que contiene una clave de indización. Para usar grafos, primero se debe definir el nodo del grafo, el cual también contiene una serie de atributos que son especificados por asociación al tipo de dato de que contiene el nodo.
  2. Extensión del nodo por derivación: cada clase nodo conforma la mínima representación que podría manejar un contenedor de nodos. Sin embargo, es posible, y a menudo muy útil, extender el nodo por derivación. Así, por ejemplo, podríamos pensar en una lista de nodos que contienen "personas". Luego podríamos mezclar distintos tipos de personas (estudiantes, profesores, empleados, etc) que serían definidos por clases derivadas de un nodo que contiene a una persona. Puesto que estudiantes, profesores, empleados, etc son personas, las primitivas que manejen nodos con personas también manejarán, sin modificación, los nodos de estudiantes, profesores, empleados, etc.

El problema fundamental de estructuras de datos

El diseño de 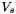$\aleph_\omega$ Aleph-w parte de la premisa de que el desempeño de un algoritmo es medida de las estructuras de datos sobre las cuales éste se sustente. En este sentido, en 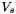$\aleph_\omega$ Aleph-w se maneja intensivamente la idea de "contenedor". Fundamentalmente, un contenedor modeliza un conjunto de elementos prácticamente en el mismo sentido que el de la teoría de conjuntos. La diferencia esencial entre un tipo de contenedor y otro es las promesas de desempeño que ofrece.

Todos los contenedores de 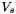$\aleph_\omega$ Aleph-w ofrecen las siguientes primitivas fundamentales cuyo nombre especifica por si mismo la índole de su función: 

 T insert(const T & item);
 T * search(const T & item);
 void remove(const T & item);
 size_t size() const;

Según la implementación y el destino para el cual se desee emplear, estas primitivas cambian ligeramente. Por ejemplo, search() podría retornar una referencia en lugar de un puntero.

Según la implementación del contenedor, éste puede exportar otras interfaces adicionales. Asumiendo un nombre de tipo genérico, Set<T>, para designar el tipo contenedor, otras primitivas que podrían exportarse son: 

  void swap(Set<T> & set);
  void join(Set<T> & set);
  void split(const T & key, Set<T> & l, Set<T> & r);
  int position(const T& key) const;
  T & select(const int pos);
  void split_pos(const int & pos, Set<T> & l, Set<T> & r);
};

swap() intercambia todos los elementos del contenedor invocante this con los del contenedor set. Lo notable de esta primitiva es que se garantiza que en todos los contenedores en los cuales se exporta la operación tomará 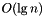$O(1)$ tanto de duración como de consumo de espacio.

join() une las elementos de this con los de set. Al final de la operación this contiene la unión, mientras que set deviene vacío.

split() particiona el conjunto this en dos conjuntos l y r tales que al final de la partición l contiene los elementos menores que key y r los mayores o iguales. Al terminar la operación this deviene vacío.

position() retorna la posición del elemento key si todos los elementos del conjunto estuviesen ordenados.

select() retorna el elemento cuya posición si el conjunto estuviese ordenado sería pos.

Comparación paramétrica

Muy parecido a la biblioteca stlc++ y otras, los contenedores 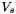$\aleph_\omega$ Aleph-w emplean una clase paramétrica (template encargada de efectuar las comparaciones entre los elementos y, según sea el caso, establecer un ordenamiento.

La estructura general de la clase de comparación es como sigue: 

 struct Cmp
 {
   bool operator () (const T & k1, const T & k2) const
   {
     // implementación de la comparación entre k1 y k2
   ]
 };

En la inmensa mayoría de los casos, la clase Cmp implementa el operador relacional "menor que". En este caso, las elementos se verían ordenado de menor a mayor. Note, sin embargo, que también se puede implementar el operador "mayor que", en cuyo caso el ordenamiento es de mayor a menor.

Todos los contenedores que emplean clase de comparación efectúan la comparación bajo el siguiente esquema: 

 if (Cmp () (p1, p2)) // equivaldría a p1 < p2
   // código si p1 < p2
 else if (Cmp() (p2, p1)) // equivaldría a p2 < p1 o p2 > p1
   // código si p2 > p1
 else
   // código si p1 == p2

Iteradores

De manera similar a la biblioteca stlc++ y otras, 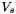$\aleph_\omega$ Aleph-w maneja como patrón de diseño el concepto de iterador sobre un conjunto. Cada contenedor de 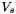$\aleph_\omega$ Aleph-w exporta una subclase llamada Iterator, cuyos métodos son esencialmente los mismos que en stlc++ pero con nombres distintos, los cuales, en la opinión de este autor, son más representativos de su función y, muy importante a decir, con menos penalidades de ejecución por múltiples instanciaciones y copias.

Para un todo contenedor que maneje algún ordenamiento, se garantiza que el iterador recorrerá los elementos de manera ordenada.

Ocultamiento parcial de la implementación

El diseño de 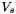$\aleph_\omega$ Aleph-w parte de la premisa de que es una biblioteca para programadores que conocen bien de estructuras de datos, algoritmos así como sus técnicas de diseño y análisis. Pensando en esto, a diferencia de otras bibliotecas, en 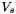$\aleph_\omega$ Aleph-w no se hace énfasis en ocultar completamente la implementación.

Hay varias razones para esta decisión. En primer lugar, en términos de desempeño, no siempre se puede garantizar la transparencia; algunas estructuras de datos y algoritmos son más lentos que otros, o consumen más espacio que otros. Estas realidades de tienden a ser patentes en la medida en que se escasean los recursos computacionales. Por esa razón, muchas de las clases, métodos y algoritmos tienen nombres que dicen parte de la implementación. Por ejemplo, el tipo DynSetAvlTree<T> connota un conjunto de elementos de tipo genérico T que es dinámico y que está implementado mediante árboles AVL. Esto contrasta con su contraparte stlc++ llamada stl::set<T>, la cual es funcionalmente equivalente y que suele implementarse con árboles AVL o rojo-negro.

Especificando con el nombre y documentación parte de la implementación le permite al programador escoger su estructura de dato, clase o algoritmo en función de lo que él considere le sea más adecuado.

De todos modos, 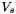$\aleph_\omega$ Aleph-w exporta el tipo Aleph::set<T>, el cual es la versión de la biblioteca stlc++.

Otra ventaja de traslucir parte de la implementación en la interfaz es que posibilita operaciones especiales según la estructura de dato. Por ejemplo, puesto que para insertar una clave en un árbol binario de búsqueda suele requerirse una búsqueda fallida, las clases basadas en árboles binarios de búsqueda exportan la interfaz search_insert(), la cual busca una clave, al cual, de no encontrarse, es insertada sin necesidad de repetir la búsqueda.

Contenedores de nodos

El siguiente grupo de clases comprende los contenedores de nodos. Tradicionalmente, los contenedores de muchas bibliotecas sólo permiten elementos uniformes y ellos mismos se encargan de manejar la memoria. Si bien este tipo de funcionalidad también está soportado, 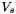$\aleph_\omega$ Aleph-w exporta una serie de contenedores cuyos elementos son nodos. Estos contenedores son árboles, diversos árboles binarios de búsqueda, tablas hash, heaps, grafos, digrafos y redes de flujo.

En la mayoría de estos contenedores el manejo de memoria es responsabilidad del usuario y no de la biblioteca. Aunque esto puede parecer engorroso, ello permite más flexibilidad de uso. Por ejemplo, se podría eliminar un nodo de un árbol e insertarlo en otro sin necesidad de eliminar y apartar de nuevo la memoria.

Cada contenedor de nodo exporta una subclase Node que es el nodo que éste emplearía.

Destructores virtuales

Considere una jerarquía de clases arbitraria derivada de un nodo. Con base a lo anterior, para albergar nodos AvlNode<Key> debemos emplear la subclase AvlTree<Key>::Node cuyo destructor no es virtual. Ahora bien, para clases derivadas de AvlTree<Key>::Node puede ser necesario invocar al destructor, lo cual es imposible desde una clase derivada de AvlTree<Key>::Node, pues su destructor no es virtual.

Para confrontar este problema, en caso de necesidad, por cada clase nodo existe una con sufijo Vtl, lo cual significa que su destructor es virtual y que por consiguiente los destructores de las clases derivadas sería invocados. El tipo contendor de nodos sería AvlTreeVtl<Key>::Node.

La razón de esta separación es que si no se requiere el destructor virtual, entonces hay una penalidad adicional de espacio por cada nodo que esté apartado. Con esta separación, el coste en espacio se paga sólo si es necesario.

Contenedores de elementos

Llegamos a un nivel final de contenedor en el cual no hay que preocuparse por nodos ni por el manejo de memoria, sino simplemente por pensar en conjuntos de elementos del mismo tipo.

Los tipos más importantes en este nivel son DynSetAvlTree, DynSetRandTree, DynSetBinTree, DynSetSplayTree, DynSetRandTree, DynSetTreap, DynLhashTable, ODhashTable<T,R>, OLhashTable, Aleph::set, Aleph::map, Aleph::multiset, Aleph::multimap, DynDlist, ArrayStack, ListStack, ArrayQueue, ListQueue, DynBinHeap, BitArray, DynArray, Aleph::vector y Aleph::list, entre otros más.

Grafos

Quizá una de las principales características de 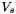$\aleph_\omega$ Aleph-w es que permite mente definir fácil y genéricamente grafos, digrafos y redes de flujo, así como ejecutar muchísimos de su algoritmos asociados sin pérdida sustancial de desempeño.

Algoritmos

Sobre la base de todos los grupos de clases previamente descritos, 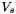$\aleph_\omega$ Aleph-w exporta una cantidad considerable de algoritmos para resolver problemas específicos, yendo desde los métodos de ordenamiento sobre arreglos y listas, pasando por una buena cantidad de algoritmos sobre grafos y redes de flujo y con una buena cantidad de algoritmos de stlc++ implementados.

Instrucciones para la instalación

Esta sección fue preparada por Alejandro Mujica.

Las dependencias son las siguientes:

Normalmente estos paquetes los descargo e instalo desde los repositorios.

Logeado como superusuario con el comando sudo su -

Luego para instalarlos escribo: 

 aptitude install build-essential gettext m4 xutils-dev libx11-dev

También se necesitan las siguientes bibliotecas que son utilizadas en Aleph:

Todos esos paquetes tienen sus propias instrucciones de instalación en un archivo de texto (puede llamarse README o INSTALL) pero en general todos (una vez descomprimidos y logeados como root) se instalan con los siguientes comandos: 

./configure
make
make install

La única diferencia es al instalar Nana, ya que una vez ejecutado el ultimo comando se debe modificar la linea 80 del archivo nana-config.h ubicado en /usr/local/include cambiando el valor de la macro ALWAYS_INCLUDE_MALLOC a 0 (cero). Por defecto viene en 1.

La biblioteca Aleph se encuentra en el sitio web del Profesor Leandro León

Una vez descargado lo descomprimen con: tar -xjvf aleph.tbz y ubican al directorio aleph (el que se descomprime) donde quieran. La convención, tanto en el curso de Diseño y Análisis de Algoritmos como en el curso de Programación 3, es instalarla en /usr/local/include y hacer un enlace simbólico de el archivo libAleph.a a /usr/local/lib

Entran al directorio aleph y ejecutan los siguientes comandos: 

xmkmf
make Makefile
make depend
make libAleph.a

Y listo.

En mi página tengo disponible para descarga un paquete que contiene Nana, GSL, GMP, MPFR, y Aleph. Lo pueden descargar aquí. Todas estas bibliotecas están en su ultima versión.

Lo descomprimen con tar -xjvf ... y saldrá el directorio Library, dentro hay un script llamado install.sh (Deben darle permiso para ejecución "chmod 755 install.sh") y si lo ejecutan logeados como superusuario (sudo ./install.sh) se instala todo automáticamente, la biblioteca Aleph se instala con la convención definida anteriormente. Esto también instala las primeras dependencias mencionadas pero es necesario que tengan conexión a Internet, si no se cuenta con esas dependencias la instalación fallará.

Pendiente por hacer

Dentro de la versión actual, 1.0, se planean:

  1. Depuraciones menores
  2. Incorporación de una clase Allocator a las clases contenedores de tipos.
  3. Refinamiento de los algoritmos de la biblioteca stlc++, especialmente la adición de la clase Allocator a los contenedores ya realizados.
  4. Culminación y depuración de los algoritmos stlc++.

Para la versión 2.0 se planea:

  1. Una implementación del simplex para redes de flujo.
  2. Mejoras en los grafos y Redes de flujo, especialmente menor consumo de memoria.
  3. Redes multiflujo
  4. Coloreado de grafos.
  5. Caminos eulerianos
  6. Heurísticas basadas en colonias de hormigas (versión 1.0 contiene una versión alfa).
  7. Planaridad de grafos.
  8. Emparejamientos mínimos y máximos
  9. Heurísticas para hamiltonianos.
  10. Gran parte de la geometría computacional.
  11. Soporte completo para la biblioteca C++11 (nueva especificación de la stlc++.
Leandro Rabindranath León