Aleph-w  1.5a.2
Biblioteca general de algoritmos y estructuras de datos
 Todo Clases Archivos Funciones Variables 'typedefs' Enumeraciones Amigas Grupos Páginas
Funciones
Algoritmos

Funciones

template<class Itor , class Operation >
Operation Aleph::for_each (Itor beg, const Itor &end, Operation op)
 
template<class Itor , class Operation >
Itor::difference_type Aleph::count_if (Itor beg, const Itor &end, Operation op)
 
template<class Itor , class T >
Itor::difference_type Aleph::count (const Itor &beg, const Itor &end, const T &value)
 
template<class Itor , class CompFunc = Aleph::less<typename Itor::value_type>>
Itor Aleph::min_element (Itor beg, const Itor &end, CompFunc op=CompFunc())
 
template<class Itor , class CompFunc = Aleph::greater<typename Itor::value_type>>
Itor Aleph::max_element (const Itor &beg, const Itor &end, CompFunc op=CompFunc())
 
template<class Itor , class UnaryPredicate >
Itor Aleph::find_if (Itor beg, const Itor &end, UnaryPredicate op)
 
template<class Itor , class T >
Itor Aleph::find (const Itor &beg, const Itor &end, const T &value)
 
template<class Itor , class Size , class T , class BinaryPredicate = Aleph::equal_to<T>>
Itor Aleph::search_n (Itor beg, const Itor &end, Size count, const T &value, BinaryPredicate op=BinaryPredicate())
 
template<class Itor1 , class Itor2 , class BinaryPredicate = Aleph::equal_to<typename Itor1::value_type>>
Itor1 Aleph::search (Itor1 beg, const Itor1 &end, Itor2 searchBeg, const Itor2 &searchEnd, BinaryPredicate op=BinaryPredicate())
 
template<class Itor1 , class Itor2 , class Comp = Aleph::equal_to<typename Itor1::value_type>>
bool Aleph::lexicographical_compare (Itor1 beg1, const Itor1 &end1, Itor2 beg2, const Itor2 &end2, Comp op=Comp())
 
template<typename Ta , template< typename > class Ca, typename Tb = Ta, template< typename > class Cb = Ca>
Cb< Tb > Aleph::map_items (const Ca< Ta > &ca, std::function< Tb(const Ta &)> operation)
 
template<template< typename > class Container, typename T , class Operation >
T Aleph::foldl (const Container< T > &container, const T &init, Operation &operation)
 
template<typename T , class Compare = Aleph::less<T>>
void Aleph::heapsort (T *array, const size_t n)
 
template<typename T , class Compare = Aleph::less<T>>
void Aleph::faster_heapsort (T *array, const size_t n)
 
template<typename T , class Compare >
void Aleph::selection_sort (T *a, const size_t n, Compare &cmp)
 
template<class Link , class Compare >
Link * Aleph::search_extreme (Link &list, Compare &cmp)
 
template<class Compare >
void Aleph::selection_sort (Dlink &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::selection_sort (Dnode< T > &list, Compare &cmp)
 
template<typename T , class Equal >
int Aleph::sequential_search (T *a, const T &x, const int l, const int r, Equal &eq)
 
template<typename T , class Equal = Aleph::equal_to<T>>
int Aleph::sequential_search (DynArray< T > &a, const T &x, const int l, const int r, Equal &eq)
 
template<typename T , class Equal = Aleph::equal_to<T>>
Dnode< T > * Aleph::sequential_search (Dnode< T > &list, const T &x, Equal &eq)
 
template<typename T , class Equal >
T * Aleph::sequential_search (DynDlist< T > &list, const T &x, Equal &eq)
 
template<typename T , class Compare = Aleph::less<T>>
int Aleph::search_extreme (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare = Aleph::less<T>>
int Aleph::search_min (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare = Aleph::greater<T>>
int Aleph::search_max (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare >
T * Aleph::search_extreme (DynDlist< T > &list, Compare &cmp)
 
template<typename T , class Compare >
T * Aleph::search_min (DynDlist< T > &list, Compare &cmp)
 
template<typename T , class Compare >
T * Aleph::search_max (DynDlist< T > &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::insertion_sort (T *a, const size_t l, const size_t r, Compare &cmp)
 
template<class Compare >
void Aleph::insert_sorted (Dlink &list, Dlink *p, Compare &cmp)
 
template<class Compare >
void Aleph::insertion_sort (Dlink &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::merge (T *a, const int l, const int m, const int r, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::mergesort (T *a, const int l, const int r, Compare &cmp)
 
template<class Tlist , class Compare >
void Aleph::merge_lists (Tlist &l1, Tlist &l2, Tlist &result, Compare &cmp)
 
template<class T , class Compare >
void Aleph::merge_lists (Dnode< T > &l1, Dnode< T > &l2, Dnode< T > &result, Compare &cmp)
 
template<class Tlist , class Compare >
void Aleph::mergesort (Tlist &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::mergesort (Dnode< T > &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::mergesort (DynDlist< T > &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::quicksort_rec (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::quicksort_rec_min (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::quicksort (T *a, const int l, const int r, Compare &cmp)
 
template<class Compare >
void Aleph::quicksort (Dlink &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::quicksort (Dnode< T > &list, Compare &cmp)
 
template<typename T , class Compare >
void Aleph::quicksort_insertion (T *a, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare >
int Aleph::random_search (T *a, const T &x, const int l, const int r, Compare &cmp)
 
template<typename T , class Compare >
Dnode< T > * Aleph::dlink_random_search (Dlink &list, const T &x, Compare &cmp)
 
template<typename T , class Compare >
Dnode< T > * Aleph::random_search (Dlink &list, const T &x, Compare &cmp)
 
template<typename T , class Compare >
T * Aleph::random_search (DynDlist< T > &list, const T &x, Compare &cmp)
 
template<typename T , class Compare >
const T & Aleph::random_select (T *a, const int i, const int n, Compare &cmp)
 
template<class Compare >
Dlink * Aleph::dlink_random_select (Dlink &list, const size_t i, Compare &cmp)
 
template<typename T , class Compare >
Dnode< T > * Aleph::random_select (Dlink &list, const size_t i, Compare &cmp)
 
template<typename T , class Compare >
T * Aleph::random_select (DynDlist< T > &list, const size_t i, Compare &cmp)
 
template<class T , class Compare >
void Aleph::selection_sort (DynArray< T > &a, Compare &cmp)
 
template<class T , class Compare >
void Aleph::bubble_sort (DynArray< T > &a, Compare &cmp)
 
template<class T , class Compare >
void Aleph::insertion_sort (DynArray< T > &a, int l, int r, Compare &cmp)
 
template<class T , class Compare >
void Aleph::shellsort (DynArray< T > &a, Compare &cmp)
 
template<class T , class Compare >
void Aleph::heapsort (DynArray< T > &a, Compare &cmp)
 
template<class T , class Compare >
void Aleph::quicksort (DynArray< T > &a, Compare &cmp)
 
template<class T , class Compare >
int Aleph::search_extreme (DynArray< T > &a, const int l, const int r, Compare &cmp)
 
template<class T , class Compare >
int Aleph::search_max (DynArray< T > &a, const int &l, const int &r, Compare &cmp)
 
template<class T , class Compare >
int Aleph::binary_search (DynArray< T > &a, const T &x, int l, int r, Compare &cmp)
 
template<class T , class Compare >
int Aleph::binary_search (DynArray< T > &a, const T &x, Compare &cmp)
 
template<typename T , class Compare >
int Aleph::binary_search_rec (T *a, const T &x, const int &l, const int &r, Compare &cmp)
 

Descripción detallada

Algoritmos genéricos

$\aleph_\omega$ Aleph-w exporta una amplia gama de algoritmos. Básicamente, las categorías de algoritmos pueden dividirse en:

  1. Ordenamientos
  2. Algoritmos que emplean contenedores $\aleph_\omega$ Aleph-w
  3. Algoritmos de la stlc++
  4. Algoritmos sobre grafos.

Con excepción de los algoritmos sobre grafos, que están agrupados bajo el móduloGrafos., todos los algoritmos están agrupados bajo esta sección. Para mirar los algoritmos sobre grafos, vaya la sección "Funciones" del módulo Grafos..

A pesar del soporte para para la biblioteca stlc++, es recomendable emplear algoritmos directos de $\aleph_\omega$ Aleph-w, pues lo de stlc++ son genéricos y según la implementación del contenedor pueden incurrir en algunas penalidades.

Autor
Leandro Rabindranath León (lrleon en ula punto ve)
Jesús Sanchez

Documentación de las funciones

template<class T , class Compare >
int Aleph::binary_search ( DynArray< T > &  a,
const T &  x,
int  l,
int  r,
Compare &  cmp 
)
inline

Búsqueda binaria sobre un arreglo dinámico ordenado.

binary_search<T,Compare>(a,x,l,r) realiza la búsqueda de x en el arreglo a comprendida entre los límites inferior l y superior r.

La rutina es genérica y utiliza dos parámetros tipo:

  1. El tipo de dato que alberga el arreglo.
  2. La clase de comparación.

La rutina usa el algoritmo de la búsqueda binaria, lo que exige que el arreglo esté ordenado. Esta condición no se verifica en el algoritmo.

El método siempre retorna un entero comprendido entre [l..r]. Si el elemento es encontrado, entonces el valor de retorno es índice donde éste se encuentra; de lo contrario, se retorna el índice donde se insertaría x para que el arreglo estuviese ordenado.

Atención
La rutina no falla si el arreglo está vacío, pero tenga cuidado con accederlo en esta situación
Parámetros
[in]ael arreglo dinámico sobre el cual realizar la búsqueda.
[in]xel elemento a buscar.
[in]líndice izquierdo de búsqueda.
[in]ríndice derecho de búsqueda.
Devuelve
índice del elemento donde se encuentra x o el índice de la posición donde se insertaría x.
Ver también
sequential_search()

Hace referencia a Aleph::DynArray< T >::access().

+ Gráfico de llamadas para esta función:

template<class T , class Compare >
int Aleph::binary_search ( DynArray< T > &  a,
const T &  x,
Compare &  cmp 
)
inline

Búsqueda binaria sobre un arreglo dinámico ordenado.

binary_search(a,x) realiza la búsqueda de x en el arreglo a comprendida entre 0 y size().

La rutina usa el algoritmo de la búsqueda binaria, lo que exige que el arreglo esté ordenado. Esta condición no se verifica en el algoritmo.

El método siempre retorna un entero comprendido entre [0..size()). Si el elemento es encontrado, entonces el valor de retorno es el índice donde éste se encuentra; de lo contrario, se retorna el índice donde se insertaría x para que el arreglo estuviese ordenado.

Atención
La rutina no falla si el arreglo está vacío, pero tenga cuidado con accederlo en esta situación
Parámetros
[in]ael arreglo dinámico sobre el cual realizar la búsqueda.
[in]xel elemento a buscar.
Devuelve
índice del elemento donde se encuentra x o el índice de la posición donde se insertaría x.
Ver también
sequential_search()

Hace referencia a Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
int Aleph::binary_search_rec ( T *  a,
const T &  x,
const int &  l,
const int &  r,
Compare &  cmp 
)
inline

Búsqueda binaria recursiva sobre un arreglo ordenado.

binary_search_rec<T,Compare>(a,x,l,r) realiza la búsqueda de x en el arreglo a comprendida entre los límites inferior l y superior r.

La rutina es genérica y utiliza dos parámetros tipo:

  1. El tipo de dato que alberga el arreglo.
  2. La clase de comparación.

La rutina usa el algoritmo de la búsqueda binaria, lo que exige que el arreglo esté ordenado. Esta condición no se verifica en el algoritmo.

El método siempre retorna un entero comprendido entre [l..r]. Si el elemento es encontrado, entonces el valor de retorno es índice donde éste se encuentra; de lo contrario, se retorna el índice donde se insertaría x para que el arreglo estuviese ordenado.

Parámetros
[in]ael arreglo sobre el cual realizar la búsqueda.
[in]xel elemento a buscar.
[in]líndice izquierdo de búsqueda.
[in]ríndice derecho de búsqueda.
Devuelve
índice del elemento donde se encuentra x o el índice de la posición donde se insertaría x.
Ver también
sequential_search()
template<class T , class Compare >
void Aleph::bubble_sort ( DynArray< T > &  a,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método de la burbuja.

bubble_sort(a) emplea el método de la burbuja para ordenar el arreglo dinámico de n elementos.

El método de la burbuja tiene un desempeño de 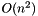$O(n^2)$. Posiblemente es el método más ineficiente de todos los existentes.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
Ver también
insertion_sort() quicksort_rec() mergesort() heapsort()

Hace referencia a Aleph::DynArray< T >::access() y Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

template<class Itor , class T >
Itor::difference_type Aleph::count ( const Itor &  beg,
const Itor &  end,
const T &  value 
)
inline

Cuenta las ocurrencias de los elementos con valor igual a value.

Parámetros
[in]begiterador al primer elemento del contenedor desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]valuevalor a comparar
Devuelve
la cantidad de elementos iguales a value

Hace referencia a Aleph::count_if().

Referenciado por Aleph::inconnected_components(), Aleph::inOrderStack(), Aleph::postOrderStack(), Aleph::preOrderStack(), Aleph::HTList::reverse(), Aleph::ODhashTable< T, Aleph::equal_to< T > >::search(), Aleph::search(), Aleph::simple_preOrderStack(), Aleph::Dlink::split_list() y Aleph::HTList::split_list().

+ Gráfico de llamadas para esta función:

+ Gráfico de llamadas a esta función:

template<class Itor , class Operation >
Itor::difference_type Aleph::count_if ( Itor  beg,
const Itor &  end,
Operation  op 
)
inline

Cuenta las ocurrencias de los elementos cuya operación op dé cierto.

Parámetros
[in]begiterador al primer elemento del contenedor.
[in]enditerador al último elemento del contenedor.
[in]opoperación a efectuar sobre cada elemento.
Devuelve
la cantidad de elementos para los cuales la operación retornó cierto.

Referenciado por Aleph::count().

+ Gráfico de llamadas a esta función:

template<typename T , class Compare >
Dnode<T>* Aleph::dlink_random_search ( Dlink &  list,
const T &  x,
Compare &  cmp 
)
inline

Búsqueda aleatoria de un elemento en una lista dlink.

dlink_random_search(list,x) se vale del algoritmo de partición del quicksort para buscar el elemento x en la lista list.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

El procedimiento tiene una complejidad esperada de $O(n \; \lg n)$, que es mayor que la mera búsqueda secuencial, pero con el añadido de que luego de la búsqueda la lista queda parcialmente ordenada.

Parámetros
[in,out]listlista en la cual se realiza la búsqueda; es parcialmente modificada luego de la búsqueda.
[in]xelemento a buscar.
Devuelve
puntero al nodo contentivo del valor x si ésta se encuentra dentro en la lista; NULL de lo contrario.
Ver también
random_search(Dlink&list,const T&x)

Hace referencia a Aleph::Dlink::append(), Aleph::Dlink::concat_list(), Aleph::Dlink::is_empty() y Aleph::Dlink::remove_next().

+ Gráfico de llamadas para esta función:

template<class Compare >
Dlink* Aleph::dlink_random_select ( Dlink &  list,
const size_t  i,
Compare &  cmp 
)

Selección aleatoria del i-ésimo elemento de una lista basada sobre Dlink.

random_select(list,i) retorna el i-ésimo menor elemento contenido en la lista list según criterio de orden determinado por la clase Compare.

La rutina se sirve de la partición del quicksort para buscar la posición i en tiempo $O(n \; \lg n)$, lo cual es un tiempo substancialmente mejor que el de la búsqueda secuencial ( $O(n^2)$).

Parámetros
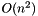[in,out]listlista donde se buscará el i-ésimo elemento. La lista queda semi-ordenado a través de las sucesivas particiones que se hayan realizado.
[in]iposición que se desea acceder.
Devuelve
puntero a Dlink correspondiente a la posición i dentro de la lista;

Hace referencia a Aleph::Dlink::append(), Aleph::Dlink::concat_list(), Aleph::Dlink::is_empty() y Aleph::Dlink::remove_next().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare = Aleph::less<T>>
void Aleph::faster_heapsort ( T *  array,
const size_t  n 
)

Ordena un arreglo por el método heapsort mejorado.

faster_heapsort(array,n) emplea una versión substancialmente mejorada del heapsort para ordenar el arreglo a de n elementos.

El heapsort tiene un desempeño garantizado de $O(n \; \lg n)$ y es estable.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Una versión sobrecargada faster_heapsort() especializa la comparación al operador "menor que" sobre el tipo T.

Parámetros
[in,out]arrayel arreglo a ordenar.
[in]nla dimensión del arreglo.
Ver también
insertion_sort() quicksort_rec() mergesort() heapsort()
selection_sort() heapsort()
template<class Itor , class T >
Itor Aleph::find ( const Itor &  beg,
const Itor &  end,
const T &  value 
)
inline

Encuentra el primer elemento de un contenedor cuyo valor sea igual a value.

Parámetros
[in]begiterador apuntando al primer elemento desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]valuevalor a encontrar. predicado.
Devuelve
iterador apuntando al miembro encontrado (si fue el caso)

Hace referencia a Aleph::find_if().

+ Gráfico de llamadas para esta función:

template<class Itor , class UnaryPredicate >
Itor Aleph::find_if ( Itor  beg,
const Itor &  end,
UnaryPredicate  op 
)
inline

Encuentra el primer elemento de un contenedor que satisfaga en predicado op.

Parámetros
[in]begiterador apuntando al primer elemento desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]opclase que determina si un elemento satisface o no el predicado.
Devuelve
iterador apuntando al miembro encontrado (si fue el caso)

Referenciado por Aleph::find().

+ Gráfico de llamadas a esta función:

template<template< typename > class Container, typename T , class Operation >
T Aleph::foldl ( const Container< T > &  container,
const T &  init,
Operation &  operation 
)
inline

Classic foldl

Let f = operation, init an initial value and container={x1,x2, ... xn}. foldl returns the result of to execute:

f(f(xn, ..., f(x2, f(x1, init))....))

template<class Itor , class Operation >
Operation Aleph::for_each ( Itor  beg,
const Itor &  end,
Operation  op 
)
inline

Ejecuta la operación op sobre cada elemento del contenedor donde esté apuntando los iterador beg y end.

Parámetros
[in]begiterador al primer elemento del contenedor desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]opoperación a efectuar sobre cada elemento.
Devuelve
una copia de la operación op
template<typename T , class Compare = Aleph::less<T>>
void Aleph::heapsort ( T *  array,
const size_t  n 
)

Ordena un arreglo por el método heapsort.

heapsort(array,n) emplea el método de heapsort para ordenar el arreglo a de n elementos.

El heapsort tiene un desempeño garantizado de $O(n \; \lg n)$ y es estable.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Una versión sobrecargada heapsort() especializa la comparación al operador "menor que" sobre el tipo T.

Parámetros
[in,out]arrayel arreglo a ordenar.
[in]nla dimensión del arreglo.
Ver también
insertion_sort() quicksort_rec() mergesort()
selection_sort() faster_heapsort()
template<class T , class Compare >
void Aleph::heapsort ( DynArray< T > &  a,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método heapsort.

heapsort(a) emplea el método de heapsort para ordenar el arreglo a de n elementos.

El heapsort tiene un desempeño garantizado de $O(n \; \lg n)$ y es estable.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
Ver también
insertion_sort() quicksort_rec() mergesort()
selection_sort() faster_heapsort()

Hace referencia a Aleph::DynArray< T >::access() y Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

template<class Compare >
void Aleph::insert_sorted ( Dlink &  list,
Dlink *  p,
Compare &  cmp 
)
inline

Inserta un nodo ordenadamente en una lista doblemente enlazada.

insert_sorted(list,p) inserta en una lista basada sobre Dlink el nodo apuntado por p.

El criterio de orden está dado por la clase de comparación Compare.

Parámetros
[in,out]listla lista a la cual se le insertará p.
[in]pel nodo a ser insertado.
Ver también
Dlink

Hace referencia a Aleph::Dlink::append() y Aleph::Dlink::Iterator::next().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
void Aleph::insertion_sort ( T *  a,
const size_t  l,
const size_t  r,
Compare &  cmp 
)
inline

Ordena un arreglo por el método de inserción.

insertion_sort(a,l,r) emplea el método de selección para ordenar el arreglo a entre los índices l y r.

El método de inserción tiene un desempeño de 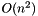$O(n^2)$. Es un método simple, por lo que consume poco tiempo constante. En promedio realiza la mitad de los intercambios que el método de selección. Su tiempo tiende a ser lineal si el arreglo está semi-ordenado. Es un buen método para arreglos pequeños y para particiones realizadas por métodos superiores pero con mayores tiempos constantes.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice izquierdo del arreglo.
[in]ríndice derecho del arreglo.
Ver también
selection_sort() quicksort_rec() mergesort() heapsort()
template<class Compare >
void Aleph::insertion_sort ( Dlink &  list,
Compare &  cmp 
)
inline

Ordena según el método de inserción una lista basada en Dlink.

insertion_sort(list) ordena según el método de inserción la lista enlazada list basada en una derivación de Dlink.

El método de inserción tiene un desempeño de 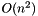$O(n^2)$.

Parámetros
[in,out]listla lista a ordenar.
Ver también
Dlink

Hace referencia a Aleph::Dlink::is_empty() y Aleph::Dlink::remove_next().

+ Gráfico de llamadas para esta función:

template<class T , class Compare >
void Aleph::insertion_sort ( DynArray< T > &  a,
int  l,
int  r,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método de inserción.

insertion_sort(a) emplea el método de selección para ordenar el arreglo dinámico a.

El método de inserción tiene un desempeño de 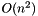$O(n^2)$. Es un método simple, por lo que consume poco tiempo constante. En promedio realiza la mitad de los intercambios que el método de selección. Su tiempo tiende a ser lineal si el arreglo está semi-ordenado. Es un buen método para arreglos pequeños y para particiones realizadas por métodos superiores pero con mayores tiempos constantes.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice izquierdo de la árte del arreglo que se desea ordenar
[in]ríndice derecho de la parte del arreglo que se desea ordenar.
Ver también
selection_sort() quicksort_rec() mergesort() heapsort()

Hace referencia a Aleph::DynArray< T >::access().

+ Gráfico de llamadas para esta función:

template<class Itor1 , class Itor2 , class Comp = Aleph::equal_to<typename Itor1::value_type>>
bool Aleph::lexicographical_compare ( Itor1  beg1,
const Itor1 &  end1,
Itor2  beg2,
const Itor2 &  end2,
Comp  op = Comp() 
)
inline

Retorna true si el rango [beg1,end1) es menor lexicográficamente que el rango [beg2,end2) según el criterio de comparación op.

template<typename Ta , template< typename > class Ca, typename Tb = Ta, template< typename > class Cb = Ca>
Cb<Tb> Aleph::map_items ( const Ca< Ta > &  ca,
std::function< Tb(const Ta &)>  operation 
)
inline

This is the classic map on a sequence.

Return a new container with each element of container mapped to the result of operation(item)

Nota
The name has been changed because clashes with the stl and Aleph and std map containers.
template<class Itor , class CompFunc = Aleph::greater<typename Itor::value_type>>
Itor Aleph::max_element ( const Itor &  beg,
const Itor &  end,
CompFunc  op = CompFunc() 
)
inline

Retorna el mayor elemento del contenedor que involucra a los iteradores.

Parámetros
[in]begiterador apuntando al primer elemento desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]opclase de comparación
Devuelve
un iterador posicionado sobre el mayor elemento.

Hace referencia a Aleph::min_element().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
void Aleph::merge ( T *  a,
const int  l,
const int  m,
const int  r,
Compare &  cmp 
)
inline

Mezcla dos particiones ordenadas almacenadas en un arreglo.

merge() asume como entrada dos particiones ordenadas entre los rangos [l..m] y [m+1..r] y las mezcla en un ordenamiento entre [l..r].

Parámetros
[in]ael arreglo
[in]líndice izquierdo del arreglo
[in]mcentro del arreglo, de la partición
[in]ríndice derecho del arreglo
template<class Tlist , class Compare >
void Aleph::merge_lists ( Tlist &  l1,
Tlist &  l2,
Tlist &  result,
Compare &  cmp 
)
inline

Mezcla dos listas ordenadas en una sola.

merge_lists(l1,l2,result) toma dos listas ordenadas l1 y l2 y las fusiona en una sola lista ordenada result según criterio de comparación Compare.

No se verifica si las listas l1 y l2 están ordenadas. Resultados serán incorrectos si no se cumple esta premisa.

Parámetros
[in,out]l1una lista ordenada a fusionar.
[in,out]l2una lista ordenada a fusionar.
[out]resultla lista donde se colocará el resultado.
template<class T , class Compare >
void Aleph::merge_lists ( Dnode< T > &  l1,
Dnode< T > &  l2,
Dnode< T > &  result,
Compare &  cmp 
)
inline

Mezcla dos listas ordenadas de tipo Dnode en una sola.

merge_lists(l1,l2,result) toma dos listas ordenadas l1 y l2 y las fusiona en una sola lista ordenada result según criterio de comparación Compare.

No se verifica si las listas l1 y l2 están ordenadas. Resultados serán incorrectos si no se cumple esta premisa.

Parámetros
[in,out]l1una lista ordenada a fusionar.
[in,out]l2una lista ordenada a fusionar.
[out]resultla lista donde se colocará el resultado.
template<typename T , class Compare >
void Aleph::mergesort ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Ordena un arreglo por el método de mezcla.

mergesort(a,l,r) ordena el arreglo a entre los índices l y r según el método de mezcla según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.

  2. Compare: clase de comparación.

    Este método tiene un desempeño de $O(n \; \lg n)$, pero un consumo de espacio de $O(n)$.

    Parámetros
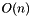    [in,out]ael arreglo a ordenar.
    [in]líndice inferior.
    [in]ríndice superior.
    Ver también
    selection_sort() insertion_sort() quicksort_rec() heapsort()
template<class Tlist , class Compare >
void Aleph::mergesort ( Tlist &  list,
Compare &  cmp 
)
inline

Ordena una lista según el método de mezcla (mergesort).

Ordena mediante el método de mezcla (mergesort) una lista basada en Dlink, según criterio de comparación Compare.

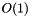Este método tiene un desempeño determinista de $O(n \; \lg n)$ y un consumo de espacio de $O(1)$. Es un muy buen método para listas.

Parámetros
[in,out]listla lista a ser ordenada.
Ver también
mergesort(Dnode<T> & list)
template<typename T , class Compare >
void Aleph::mergesort ( Dnode< T > &  list,
Compare &  cmp 
)
inline

Ordena una lista según el método de mezcla (mergesort).

Ordena mediante el método de mezcla (mergesort) una lista basada en Dnode<T>, según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

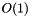Este método tiene un desempeño determinista de $O(n \; \lg n)$ y un consumo de espacio de $O(1)$. Es un muy buen método para listas.

Parámetros
[in,out]listla lista a ser ordenada.
Ver también
mergesort(Dlink & list) quicksort(Dnode<T>)
template<typename T , class Compare >
void Aleph::mergesort ( DynDlist< T > &  list,
Compare &  cmp 
)
inline

Ordena una lista dinámica según el método de mezcla (mergesort).

Ordena mediante el método de mezcla (mergesort) una lista dinámica según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

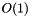Este método tiene un desempeño determinista de $O(n \; \lg n)$ y un consumo de espacio de $O(1)$. Es un muy buen método para listas.

Parámetros
[in,out]listla lista a ser ordenada.
Ver también
quicksort(DynDlist<T> & list)
template<class Itor , class CompFunc = Aleph::less<typename Itor::value_type>>
Itor Aleph::min_element ( Itor  beg,
const Itor &  end,
CompFunc  op = CompFunc() 
)
inline

Retorna el menor elemento del contenedor que involucra a los iteradores.

Parámetros
[in]begiterador apuntando al primer elemento desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]opclase de comparación
Devuelve
un iterador posicionado sobre el menor elemento.

Referenciado por Aleph::max_element().

+ Gráfico de llamadas a esta función:

template<typename T , class Compare >
void Aleph::quicksort ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Ordena un arreglo por el método quicksort sin recursión.

quicksort_rec(a,l,r) ordena el arreglo a entre los índices l y r según el método quicksort según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Esta versión de quicksort puede ocupar espacio 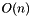$O(n)$. Utilice quicksort_rec_min() si se desea garantizar un consumo máximo de espacio de 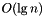$O(\lg n)$ en detrimento de un poco más de tiempo constante.

El quicksort es un método probabilístico. En un muy mal caso -muy mala suerte- puede degradarse a 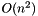$O(n^2)$. Para paliar, en la medida de la suerte, los malos casos, use quicksort_insertion() que ejecuta heurísticas para paliar los malos casos e invoca al método de inserción para particiones del arreglo pequeñas.

Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice inferior.
[in]ríndice superior.
Ver también
selection_sort() insertion_sort() mergesort() heapsort()
quicksort_rec_min() quicksort_insertion() quicksort_rec()

Hace referencia a Aleph::FixedStack< T >::pop(), Aleph::FixedStack< T >::push() y Aleph::FixedStack< T >::size().

Referenciado por Aleph::Map_Matrix_Graph< GT, SA >::copy_list_graph().

+ Gráfico de llamadas para esta función:

+ Gráfico de llamadas a esta función:

template<class Compare >
void Aleph::quicksort ( Dlink &  list,
Compare &  cmp 
)

Ordena una lista enlazada por el método quicksort.

quicksort(list) ordena una lista según el método quicksort según criterio de comparación Compare.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Parámetros
[in,out]listla lista a ordenar.

Hace referencia a Aleph::Dlink::append(), Aleph::Dlink::concat_list(), Aleph::Dlink::is_empty(), Aleph::Dlink::is_unitarian_or_empty() y Aleph::Dlink::remove_next().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
void Aleph::quicksort ( Dnode< T > &  list,
Compare &  cmp 
)

Ordena una lista por el método quicksort.

quicksort(list) ordena una lista mediante el método quicksort según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Esta primitiva puede usarse para listas de tipo Dlist y DynDlist.

Parámetros
[in,out]listla lista a ordenar.
Ver también
Dnode Dlist DynDlist
template<class T , class Compare >
void Aleph::quicksort ( DynArray< T > &  a,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método quicksort sin recursión.

quicksort(a) ordena el arreglo dinámico según el método quicksort según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Esta versión de quicksort ocupa espacio máximo de 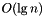$O(\lg n)$.

El quicksort es un método probabilístico. En un muy mal caso -muy mala suerte- puede degradarse a 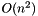$O(n^2)$. Para paliar, en la medida de la suerte, los malos casos, use quicksort_insertion() que ejecuta heurísticas para paliar los malos casos e invoca al método de inserción para particiones del arreglo pequeñas.

Parámetros
[in,out]ael arreglo a ordenar.
Ver también
selection_sort() insertion_sort() heapsort()
quicksort_rec_min() quicksort_insertion() quicksort_rec()

Hace referencia a Aleph::FixedStack< T >::is_empty(), Aleph::FixedStack< T >::pop() y Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
void Aleph::quicksort_insertion ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Ordena un arreglo por el método quicksort mejorado.

quicksort_insertion(a,l,r) ordena el arreglo a entre los índices l y r según el método quicksort según criterio de comparación Compare.

El procedimiento combina diversas técnicas para acelerar el ordenamiento y a la vez evitar degradación por malos casos.

Los malos casos son tratados mediante una selección del pivote consistente de la mediana entre l, r y el centro de la partición.

Para asegurar un consumo máximo de pila de 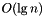$O(\lg n)$, el método siempre procede recursivamente a ordenar la partición más pequeña.

Cuando la partición alcanza un tamaño menor o igual a la constante global Aleph::Insertion_Threshold, entonces la partición es ordenada por el método de inserción, el cual es más rápido que el quicksort para tamaños pequeños.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice inferior.
[in]ríndice superior.
Ver también
insertion_sort() mergesort() heapsort()
quicksort_rec_min() quicksort_insertion() quicksort()
template<typename T , class Compare >
void Aleph::quicksort_rec ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Ordena un arreglo por el método quicksort.

quicksort_rec(a,l,r) ordena el arreglo a entre los índices l y r según el método quicksort según criterio de comparación Compare.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

Este método tiene un desempeño esperado de $O(n \; \lg n)$ y es considerado el método de ordenamiento más veloz.

Esta versión de quicksort puede ocupar espacio 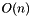$O(n)$. Utilice quicksort_rec_min() si se desea garantizar un consumo máximo de espacio de 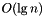$O(\lg n)$ en detrimento de un poco más de tiempo constante.

El quicksort es un método probabilístico. En un muy mal caso -muy mala suerte- puede degradarse a 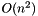$O(n^2)$. Para paliar, en la medida de la suerte, los malos casos, use quicksort_insertion() que ejecuta heurísticas para paliar los malos casos e invoca al método de inserción para particiones del arreglo pequeñas.

Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice inferior.
[in]ríndice superior.
Ver también
selection_sort() insertion_sort() mergesort() heapsort()
quicksort_rec_min() quicksort_insertion() quicksort()
template<typename T , class Compare >
void Aleph::quicksort_rec_min ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Ordena un arreglo según el método quicksort con mínimo consumo de espacio.

El quicksort puramente recursivo puede consumir pila proporcional al tamaño del arreglo a ordenar. Para evitar este problema, en detrimento de un ligero coste de ejecución, quicksort_rec_min() siempre ordena de primero la partición más pequeña. Por los demás, las mismas consideraciones que para quicksort_rec() aplican.

Parámetros
[in,out]ael arreglo a ordenar.
[in]líndice inicial por donde se ordena.
[in]ríndice final por donde se ordena.
Ver también
quicksort_rec() quicksort() quicksort_insertion()
template<typename T , class Compare >
int Aleph::random_search ( T *  a,
const T &  x,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Búsqueda aleatoria de un elemento en un arreglo.

random_search(a,x,l,r) se vale del algoritmo de partición del quicksort para buscar el elemento x en el arreglo a comprendido entre los límites l y r.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.

  2. Compare: clase de comparación.

    El procedimiento tiene una complejidad esperada de $O(n \; \lg n)$, que es mayor que la mera búsqueda secuencial, pero con el añadido de que luego de la búsqueda el arreglo queda parcialmente ordenado y, puesto que la selección del pivote es la mediana entre l, r y el centro del arreglo, la búsqueda tiende a ser lineal a medida que se hacen más búsquedas aleatorias.

    Parámetros
    [in,out]aarreglo a buscar; es parcialmente modificado luego de la búsqueda.
    [in]xelemento a buscar.
    [in]líndice inferior de comienzo de la búsqueda.
    [in]ríndice superior de término de la búsqueda.
    Devuelve
    índice de una entrada del arreglo contentiva del valor x si ésta se encuentra dentro del arreglo; Not_Found (por general -1) de lo contrario.
    Ver también
    sequential_search() binary_search_rec()
template<typename T , class Compare >
Dnode<T>* Aleph::random_search ( Dlink &  list,
const T &  x,
Compare &  cmp 
)

Búsqueda aleatoria de un elemento en una lista Dnode<T>.

random_search(list,x) se vale del algoritmo de partición del quicksort para buscar el elemento x en la lista list.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

El procedimiento tiene una complejidad esperada de $O(n \; \lg n)$, que es mayor que la mera búsqueda secuencial, pero con el añadido de que luego de la búsqueda la lista queda parcialmente ordenada.

Una especialización usa la relación "menor que" como criterio de comparación y ahorra la escritura de esa clase.

Parámetros
[in,out]listlista en la cual se realiza la búsqueda; es parcialmente modificada luego de la búsqueda.
[in]xelemento a buscar.
Devuelve
puntero al nodo contentivo del valor x si ésta se encuentra dentro en la lista; NULL de lo contrario.
Ver también
dlink_random_search
template<typename T , class Compare >
T* Aleph::random_search ( DynDlist< T > &  list,
const T &  x,
Compare &  cmp 
)
inline

Búsqueda aleatoria de un elemento en una lista dinámica.

random_search(list,x) se vale del algoritmo de partición del quicksort para buscar el elemento x en la lista dinámica list.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.

El procedimiento tiene una complejidad esperada de $O(n \; \lg n)$, que es mayor que la mera búsqueda secuencial, pero con el añadido de que luego de la búsqueda la lista queda parcialmente ordenada.

Una especialización usa la relación "menor que" como criterio de comparación y ahorra la escritura de esa clase.

Parámetros
[in,out]listlista dinámica en la cual se realiza la búsqueda; es parcialmente modificada luego de la búsqueda.
[in]xelemento a buscar.
Devuelve
puntero x dentro de la lista si ésta se encuentra dentro de ella; NULL de lo contrario.
Ver también
DynDlist
template<typename T , class Compare >
const T& Aleph::random_select ( T *  a,
const int  i,
const int  n,
Compare &  cmp 
)

Selección aleatoria del i-ésimo elemento de un arreglo.

random_select(a,i,n) retorna el i-ésimo menor elemento contenido en el arreglo a de dimensión n.

La rutina se sirve de la partición del quicksort para buscar la posición i en tiempo $O(n \; \lg n)$, lo cual es un tiempo substancialmente mejor que el de la búsqueda secuencial ( $O(n^2)$).

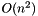El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]aarreglo donde se buscará el i-ésimo elemento. El arreglo queda semi-ordenado a través de las sucesivas particiones que se hayan realizado.
[in]iposición que se desea acceder.
[in]ndimensión del arreglo
Excepciones
out_of_rangesi i es mayor o igual a n.
template<typename T , class Compare >
Dnode<T>* Aleph::random_select ( Dlink &  list,
const size_t  i,
Compare &  cmp 
)

Selección aleatoria del i-ésimo elemento de una lista basada sobre Dlink.

random_select(list,i) retorna el i-ésimo menor elemento contenido en la lista list.

La rutina se sirve de la partición del quicksort para buscar la posición i en tiempo $O(n \; \lg n)$, lo cual es un tiempo substancialmente mejor que el de la búsqueda secuencial ( $O(n^2)$).

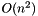El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]listlista donde se buscará el i-ésimo elemento. La lista queda semi-ordenado a través de las sucesivas particiones que se hayan realizado.
[in]iposición que se desea acceder.
Devuelve
puntero a Dlink correspondiente a la posición i dentro de la lista; NULL si i está fuera de rango.
template<typename T , class Compare >
T* Aleph::random_select ( DynDlist< T > &  list,
const size_t  i,
Compare &  cmp 
)

Selección aleatoria del i-ésimo elemento de una lista dinámica.

random_select(list,i) retorna el i-ésimo menor elemento contenido en la lista dinámica list.

La rutina se sirve de la partición del quicksort para buscar la posición i en tiempo $O(n \; \lg n)$, lo cual es un tiempo substancialmente mejor que el de la búsqueda secuencial ( $O(n^2)$).

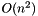El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]listlista dinámica donde se buscará el i-ésimo elemento. La lista queda semi-ordenado a través de las sucesivas particiones que se hayan realizado.
[in]iposición que se desea acceder.
Devuelve
puntero al elemento de la lista dinámica correspondiente a la posición i dentro de la lista; NULL si i está fuera de rango.
template<class Itor1 , class Itor2 , class BinaryPredicate = Aleph::equal_to<typename Itor1::value_type>>
Itor1 Aleph::search ( Itor1  beg,
const Itor1 &  end,
Itor2  searchBeg,
const Itor2 &  searchEnd,
BinaryPredicate  op = BinaryPredicate() 
)
inline

Búsqueda de subrangos.

Esta función busca entre el rango dado beg y end la primera ocurrencia exacta del subrango searchBeg y searchEnd.

De encontrarse una ocurrencia del subrango, la rutina retorna un iterador posicionado en el primer elemento de la primera ocurrencia del subrango. De lo contrario, el iterador de retorno es end.

Para comparar los elementos entre contenedores, la rutina invoca a la clase predicado op de la siguiente manera

op(*beg, *pivot)

Donde beg es la posición actual del rango de búsqueda y pivot es la posición actual en el subrango.

Nótese que el rango en el cual se busca y el subrango a buscar no sólo pueden referir a contenedores diferentes, sino, también de tipos distintos. Por ejemplo, [beg, end) podría set a un contenedor de tipo set, mientras que [searchBeg, searchEnd) a un contenedor de tipo vector.

Parámetros
[in]begiterador apuntando al primer elemento del contenedor desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]searchBegiterador apuntando al primer elemento del subrango a buscar.
[in]searchEnditerador al último elemento del subrango a buscar.
[in]opoperación de comparación entre elementos de un rango.
Devuelve
si el subrango es encontrado, iterador posicionado sobre el primer elemento de la primera ocurrencia del subrango. De lo contrario end.
Nota
Muy importante a notar que a través de op se puede instrumentar contenedores distintos, de clase distinta y con elementos de diferentes tipos.

Hace referencia a Aleph::count().

Referenciado por Aleph::OLhashTable< std::pair< Key, Data >, Cmp >::remove() y Aleph::DynHashTable< std::pair< Key, Data >, Cmp, LhashTable >::search().

+ Gráfico de llamadas para esta función:

+ Gráfico de llamadas a esta función:

template<class Link , class Compare >
Link* Aleph::search_extreme ( Link &  list,
Compare &  cmp 
)
inline

Búsqueda genérica de un elemento extremo en una lista de nodos Dlink.

search_extreme(list) busca secuencialmente en la lista de nodos list el elemento extremo, mínimo o máximo según el criterio de comparación Compare.

Parámetros
[in]listla lista sobre la cual realizar la búsqueda.
Devuelve
puntero al nodo contentivo del elemento extremo.
Nota
No se verifica si la lista está vacía.
template<typename T , class Compare = Aleph::less<T>>
int Aleph::search_extreme ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Búsqueda genérica en un arreglo de un elemento extremo.

search_extreme(a, l, r) busca secuencialmente en el arreglo a, entre los índices l y r, el elemento extremo, mínimo o máximo según el criterio de comparación Compare.

Parámetros
[in]ael arreglo sobre el cual realizar la búsqueda.
[in]líndice de comienzo de la búsqueda.
[in]ríndice de término de la búsqueda.
Devuelve
índice contentivo del extremo.
Nota
No se verifica si la secuencia está vacía.
template<typename T , class Compare >
T* Aleph::search_extreme ( DynDlist< T > &  list,
Compare &  cmp 
)
inline

Búsqueda genérica de un elemento extremo en una lista de nodos (Dlist<T>).

search_extreme(list) busca secuencialmente en la lista de nodos list el elemento extremo, mínimo o máximo según el criterio de comparación Compare.

Parámetros
[in]listla lista sobre la cual realizar la búsqueda.
Devuelve
puntero al nodo contentivo del elemento extremo.
Nota
No se verifica si la lista está vacía.

Hace referencia a Aleph::Dnode< T >::get_data().

+ Gráfico de llamadas para esta función:

template<class T , class Compare >
int Aleph::search_extreme ( DynArray< T > &  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Búsqueda genérica en un arreglo dinámico de un elemento extremo.

search_extreme(a, l, r) busca secuencialmente en el arreglo a, entre los índices l y r, el elemento extremo, mínimo o máximo según el criterio de comparación Compare.

Parámetros
[in]ael arreglo sobre el cual realizar la búsqueda.
[in]líndice de comienzo de la búsqueda.
[in]ríndice de término de la búsqueda.
Devuelve
índice contentivo del extremo.
Nota
No se verifica si la secuencia está vacía.

Hace referencia a Aleph::DynArray< T >::access().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare = Aleph::greater<T>>
int Aleph::search_max ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Retorna el máximo elemento del arreglo a entre l y r.

template<typename T , class Compare >
T* Aleph::search_max ( DynDlist< T > &  list,
Compare &  cmp 
)
inline

Retorna el máximo elemento de la lista list.

template<class T , class Compare >
int Aleph::search_max ( DynArray< T > &  a,
const int &  l,
const int &  r,
Compare &  cmp 
)
inline

Retorna el máximo elemento del arreglo a entre l y r.

template<typename T , class Compare = Aleph::less<T>>
int Aleph::search_min ( T *  a,
const int  l,
const int  r,
Compare &  cmp 
)
inline

Retorna el mínimo elemento del arreglo a entre l y r.

template<typename T , class Compare >
T* Aleph::search_min ( DynDlist< T > &  list,
Compare &  cmp 
)
inline

Retorna el mínimo elemento de la lista list.

template<class Itor , class Size , class T , class BinaryPredicate = Aleph::equal_to<T>>
Itor Aleph::search_n ( Itor  beg,
const Itor &  end,
Size  count,
const T &  value,
BinaryPredicate  op = BinaryPredicate() 
)
inline

Retorna la posición del primero de los count elementos consecutivos que se encuentre en el rango beg y end para el cual un predicado es cierto.

El predicado es invocado como:

op () (item, value)
Parámetros
[in]begiterador apuntando al primer elemento del contenedor desde donde se desea iniciar la búsqueda.
[in]enditerador al último elemento del contenedor.
[in]countcantidad de ocurrencias consecutivas que se desea buscar.
[in]valuevalor específico del elemento a buscar.
[in]opcriterio de comparación
Devuelve
un iterador posicionado en el primer elemento encontrado o end si no existe count ocurrencias.
template<typename T , class Compare >
void Aleph::selection_sort ( T *  a,
const size_t  n,
Compare &  cmp 
)
inline

Ordena un arreglo por el método de selección.

selection_sort(a,n) emplea el método de selección para ordenar el arreglo a de n elementos.

El método de selección tiene un desempeño de 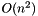$O(n^2)$. Debido a su simplicidad de implantación, su coste constante es bajo, por lo que es un buen método para arreglos de dimensión muy pequeña.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
[in]nla dimensión del arreglo.
Ver también
insertion_sort() quicksort_rec() mergesort() heapsort()
template<class Compare >
void Aleph::selection_sort ( Dlink &  list,
Compare &  cmp 
)
inline

Ordena por el método de selección una lista doblemente enlazada.

selection_sort(list) sobre una lista derivada de Dlink ordena mediante el método de selección la lista list.

La rutina requiere el parámetro tipo Compare que instrumenta la comparación entre los miembros de la lista. Compare se invoca como Compare()(l1,l2), donde l1 y l2 son dos enlaces de tipo Dlink. El usuario es responsable de instrumentar adecuadamente Compare()() de modo que se accedan los campos de interés y se efectúe la comparación.

Parámetros
[in,out]listlista a ser ordenada.

Hace referencia a Aleph::Dlink::append(), Aleph::Dlink::del() y Aleph::Dlink::is_empty().

+ Gráfico de llamadas para esta función:

template<typename T , class Compare >
void Aleph::selection_sort ( Dnode< T > &  list,
Compare &  cmp 
)
inline

Ordena una lista enlazada de tipo Dnode<T> mediante el método de selección.

Ordena la lista list, con nodos de tipo Dnode<T> según el método de selección.

El método de selección tiene un desempeño de 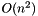$O(n^2)$. Debido a su simplicidad de implantación su coste constante es bajo, por lo que es un buen método para arreglos de dimensión muy pequeña.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]listka lista a ser ordenada.
template<class T , class Compare >
void Aleph::selection_sort ( DynArray< T > &  a,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método de selección.

selection_sort(a) emplea el método de selección para ordenar el arreglo dinámico de n elementos.

El método de selección tiene un desempeño de 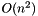$O(n^2)$. Debido a su simplicidad de implantación, su coste constante es bajo, por lo que es un buen método para arreglos de dimensión muy pequeña.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
Ver también
insertion_sort() quicksort_rec() mergesort() heapsort()

Hace referencia a Aleph::DynArray< T >::access() y Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

template<typename T , class Equal >
int Aleph::sequential_search ( T *  a,
const T &  x,
const int  l,
const int  r,
Equal &  eq 
)
inline

Búsqueda secuencial sobre un arreglo.

sequential_search(a,x,l,r) busca secuencialmente, en el arreglo a, entre los índices l y r, respectivamente, la primera ocurrencia de x.

La función maneja dos parámetros tipo:

  1. T: el tipo de datos que alberga el arreglo.
  2. Equal: clase comparación entre los elementos.
Parámetros
[in]ael arreglo sobre el cual se realiza la búsqueda.
[in]xel elemento a buscar.
[in]líndice izquierdo donde comienza la búsqueda.
[in]ríndice derecho donde termina la búsqueda.
Devuelve
índice de la primera posición en arreglo que contiene el elemento x; -1 de lo contrario.
template<typename T , class Equal = Aleph::equal_to<T>>
int Aleph::sequential_search ( DynArray< T > &  a,
const T &  x,
const int  l,
const int  r,
Equal &  eq 
)
inline

Búsqueda secuencial sobre un arreglo dinámico.

sequential_search(a,x,l,r) busca secuencialmente, en el arreglo a, entre los índices l y r, respectivamente, la primera ocurrencia de x.

La función maneja dos parámetros tipo:

  1. T: el tipo de datos que alberga el arreglo.
  2. Equal: clase comparación entre los elementos.

Esta versión sobre arreglos dinámicos salta las posiciones que con certeza no han sido escritas. Sin embargo, tómese en consideración que, según el tamaño del bloque, pueden haber entradas no escritas pero circunscritas en direcciones de memoria válidas. En este sentido, es posible que dentro de aquella clase de entradas se encuentre un elemento con valor x.

Parámetros
[in]ael arreglo dinámico sobre el cual se realiza la búsqueda.
[in]xel elemento a buscar.
[in]líndice izquierdo donde comienza la búsqueda.
[in]ríndice derecho donde termina la búsqueda.
Devuelve
índice de la primera posición en arreglo que contiene el elemento x; -1 de lo contrario.
Nota
La búsqueda no puede distinguir si una entrada válida ha sido escrita o no. La programación de la clase Equal puede considerar un valor especial que represente que la entrada no ha sido escrita. Se garantiza que entrada que no haya sido mapeada en un bloque no será accedida.
Ver también
DynArray

Hace referencia a Aleph::DynArray< T >::access() y Aleph::DynArray< T >::exist().

+ Gráfico de llamadas para esta función:

template<typename T , class Equal = Aleph::equal_to<T>>
Dnode<T>* Aleph::sequential_search ( Dnode< T > &  list,
const T &  x,
Equal &  eq 
)
inline

Búsqueda secuencial sobre una lista de nodos.

sequential_search(list,x) busca secuencialmente, en la lista de nodos de tipo Dnode<T> list la primera ocurrencia de x.

La función maneja dos parámetros tipo:

  1. T: el tipo de datos que alberga el arreglo.
  2. Equal: clase comparación entre los elementos.
Parámetros
[in]listla lista sobre el cual se realiza la búsqueda.
[in]xel elemento a buscar.
Devuelve
puntero al primer nodo que contiene el elemento x; NULL de lo contrario.
Ver también
Dnode
template<typename T , class Equal >
T* Aleph::sequential_search ( DynDlist< T > &  list,
const T &  x,
Equal &  eq 
)
inline

Búsqueda secuencial sobre una lista dinámica DynDlist.

sequential_search(list,x) busca secuencialmente, en la lista dinámica list (DynDlist<T>) la primera ocurrencia de x.

La función maneja dos parámetros tipo:

  1. T: el tipo de datos que alberga el arreglo.
  2. Equal: clase comparación entre los elementos.
Parámetros
[in]listla lista dinámica sobre el cual se realiza la búsqueda.
[in]xel elemento a buscar.
Devuelve
puntero al primer elemento con valor igual a x; NULL de lo contrario.
Ver también
DynDlist

Hace referencia a Aleph::Dnode< T >::get_data().

+ Gráfico de llamadas para esta función:

template<class T , class Compare >
void Aleph::shellsort ( DynArray< T > &  a,
Compare &  cmp 
)
inline

Ordena un arreglo dinámico por el método de shell.

shellsort(a) emplea el método de selección para ordenar el arreglo dinámico a.

El método shell tiende a un desempeño de 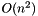$O(n^2)$, pero en la práctica es considerablemente menor.

El método emplea dos parámetros tipo:

  1. T: el tipo de elementos que tiene el arreglo.
  2. Compare: clase de comparación.
Parámetros
[in,out]ael arreglo a ordenar.
Ver también
selection_sort() quicksort_rec() mergesort() heapsort()

Hace referencia a Aleph::DynArray< T >::access() y Aleph::DynArray< T >::size().

+ Gráfico de llamadas para esta función:

Leandro Rabindranath León