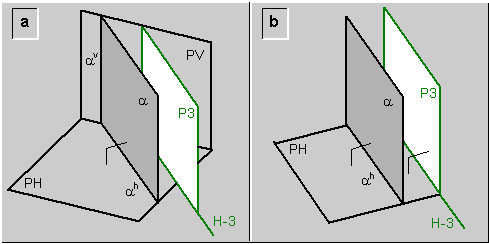
Si un plano (a) se encuentra en posición vertical con respecto a un sistema (H-V) de doble proyección ortogonal. Puede establecerse un nuevo sistema (H-3) de doble proyección ortogonal, con respecto al cual el plano (a) sea un plano vertical, cambiando el plano vertical de proyección (PV) por un plano tres de proyección (P3) que sea paralelo al plano (a)\ fig.10a y fig.10b.

 

 

La traza horizontal del plano (a) es común a ambos sistemas, y su proyección horizontal (a^h) es paralela a la nueva línea de tierra (H-3).

 

En este nuevo sistema (H-3) de doble proyección ortogonal, el plano (a) se proyecta sobre el plano tres de proyección (P3) en verdadero tamaño, siendo esta la razón de realizar el cambio del plano vertical de proyección.

 

 

Ejemplo: Definir las proyecciones del cuadrado (A;B;C;D), contenido en el plano (a) y en el (I) cuadrante\ fig.11a.

 

Solución:

 

a)     Por ser el plano (a) un plano vertical, se definen, sobre la proyección horizontal (a^h) de su traza horizontal, las proyecciones horizontales (A^h y B^h) de los puntos (A y B)\ fig.11b.

Se efectúa el cambio del plano vertical de proyección por el plano tres de proyección (P3), paralelo al plano (a); representa este cambio de plano de proyección, la nueva línea de tierra (H-3), paralela a la proyección horizontal (a^h) de la traza horizontal del plano (a).

Se definen, mediante el traslado de sus cotas (Z_A y Z_B), las proyecciones (A³ y B³) de los puntos (A y B) sobre el plano tres de proyección (P3).

 

 

b)    Se dibuja, en verdadero tamaño, el cuadrado (A³; B³; C³; D³), con lado en (A³; B³)\ fig.11c.

c)     Se definen las proyecciones vertical y horizontal del cuadrado (A; B; C; D)\ fig.11d.

---