 |
 |
 |
|
|
|
ÁLGEBRA MATRICIAL
PROF. MARIELA SARMIENTO
SESIÓN 1: VECTORES EN EL PLANO
RESUMEN
Un vector es un segmento de recta orientado que va desde un punto inicial P hasta un punto final Q y lo denotamos por
Al trasladar un vector al origen, obtenemos otro vector llamado representación posicional de dicho vector, que no es más que el vector con punto inicial en el origen del plano y punto final en algún A(a1,a2), tal que ambos vectores tienen la misma longitud (magnitud), dirección y sentido.
La magnitud del vector A viene dada por:
La dirección del vector A viene dada por el ángulo director (ángulo medido desde el eje positivo x hasta el vector A, en sentido positivo):
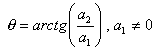
Los vectores pueden sumarse, restarse o multiplicarse por un escalar, esto es:
Suma : A + B = (a1 , a2) + (b1 , b2) = (a1+b1 , a2+b2)
Resta: A – B = (a1 – b1 , a2 – b2)
Multiplicación por un escalar: aA = a (a1 , a2) = (aa1 , aa2)
|
|
|
PAGINAS SIMILARES |
AUTOEVALUACIÓN |
Profa. Mariela Sarmiento SantanaDra.
en Pedagogía
|
|
|
|
 |
