El comando dsolve

• En esta hoja de trabajo vamos a mostrar algunas posibildades adicionales que ofrece el Maple  cuando trabajamos en la solución de ecuaciones diferenciales.

Obtener una solución para una ecuación diferencial puede algunas veces resultar en un proceso bastante simple, es solo cuestion de pedirle al programa que nos busque  la solución, como se muestra en el siguiente ejemplo.

>	restart;with(DEtools):

Se escribe la ecuación diferencial,

>	ed1:= diff(y(x),x) = x^2*y(x);

y con el comando "dsolve" pedimos la solución. El maple la escribira siempre y cuando esto sea posible.

>	sol:=dsolve(ed1,y(x));

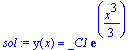
Es importante notar que podemos sacar mas información de todo este proceso, como por ejemplo preguntar por el tipo de ecuación diferencial en cuestión

>	odeadvisor(ed1);

Asi como pedirle el programa que verifique si es en relidad una solución de la ecuación diferencial.

>	odetest(sol,ed1);

Existe tambien la posiblidad del que Maple  nos vaya mostrando en pantalla las técnicas que esta utilizando durante el proceso de la busqueda de una solución. La manera de proceder es activando la opción "linfolevel". Para mayor información escriba:

> ?infolevel

>	infolevel[dsolve] := 5:

Consideremos la siguiente ecuación diferencial:

>	ed2 := sin(x)*diff(y(x),x)-cos(x)*y(x)+a=0;

A simple vista notamos que es una ecuación diferencial lineal de primer orden, pero de todos modos preguntemos por su clasificación

>	odeadvisor(ed2);

Como sabemos exactamente del tipo de ecuacion que estamos considrando le podemos pedirle a Maple   que vaya directamente  al grano cuando busque la solución

>	dsolve(ed2, [linear]);

Classification methods on request

Methods to be used are: [linear]

----------------------------

* Tackling ODE using method: linear

--- Trying classification methods ---

trying 1st order linear

<- 1st order linear successful

Ahora tenemos en pantalla los metodos utilizados por el programa cuando se buscaba la solución.

Estudiemos otro ejemplo, en este caso una ecuación diferencial no lineal de primer orden pero que no es exacta

>	ed3 := diff(y(x),x) = 2*a/x^2/(-y(x)+2*((x*y(x)^2-4*a)/x)*a);

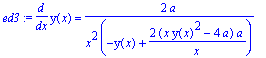
>	odeadvisor(ed3);

-> The symmetry found is, [exp(4*a*y)*x^2, 0]

>	odeadvisor(ed3,[exact]);

Tambien podemos averiguar que no es exacta porque al pedir su solución utilizando un algoritmo para ecuaciones exactas el programa falla

>	dsolve(ed3, [exact]);

Classification methods on request

Methods to be used are: [exact]

----------------------------

* Tackling ODE using method: exact

--- Trying classification methods ---

trying exact

Veamos si existe un factor integrante

>	mu := intfactor(ed3);

   -> Computing symmetries using: way = 2

   -> Computing symmetries using: way = 3

   <- successful computation of symmetries.

Sabemos que si multiplicamos la ecuación diferencial por este factor integrante se convertirá en una ecuación diferencial exacta

>	dsolve( mu*ed3,[exact]);

Classification methods on request

Methods to be used are: [exact]

----------------------------

* Tackling ODE using method: exact

--- Trying classification methods ---

trying exact

<- exact successful

>	odetest(%,ed3);

Consideremos una ecuación diferencial más compleja

>	ed4 := diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x)=0;

>	odeadvisor(ed4,[exact]);

>	odeadvisor(ed4);

>	sol:=dsolve(ed4);

Methods for first order ODEs:

--- Trying classification methods ---

trying a quadrature

trying 1st order linear

trying Bernoulli

trying separable

trying inverse linear

trying homogeneous types:

trying Chini

Chini's absolute invariant is:, 1/4*sin(x)^2*(-1+2*cos(x))^2/cos(x)^3

differential order: 1; looking for linear symmetries

trying exact

Looking for potential symmetries

trying Riccati

trying Riccati sub-methods:

   <- Riccati with symmetry of the form [0, exp(-Int(f,x))/P*(y*P-f)^2] successful

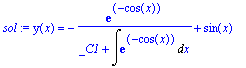
>	odetest(sol,ed4);

Para solicitar más información sobre las ecuaciones del tipo Riccati se escribe lo siguiente

>	odeadvisor(ed4, help);

Este ultimo comando nos abrirá una nueva ventana con mucha más información sobre las ecuaciones diferenciales del tipo Riccati.

Sabemos tambien que si quitamos el ultimo termino de la ecuación diferencial anterior la ecuación pasa a ser una ecuación diferencial del tipo Bernoulli

>	ed5:=diff(y(x),x)-y(x)^2+y(x)*sin(x)=0;

>	sol:=dsolve(ed5);

Methods for first order ODEs:

--- Trying classification methods ---

trying a quadrature

trying 1st order linear

trying Bernoulli

<- Bernoulli successful

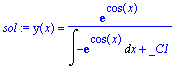
>	odetest(sol,ed5);

Si no queremos que   Maple  no siga mostrando en pantalla la información para el usuario apagamos la opcion "infolevel" de la siguiente manera

>	infolevel[dsolve] := 0:

>	ed6:=diff(y(x),x)-y(x)+y(x)*sin(x);

>	dsolve(ed6);

>	odetest(%,ed6);

>

Fin.