POTENCIAS DE LA UNIDAD IMAGINARIA i
 
  Las distintas potencias de la unidad imaginaria se obtienen de las cuatro relaciones fundamentales

i¹ = i, i ² = -1, i ³ = - i, i ⁴ = 1.

 

Si queremos calcular, por ejemplo i ²⁷, dividimos 27 entre 4 tendremos que 27 = 4 (6) + 3. Luego

i ²⁷  =  i ^{4 (6) + 3} = (i ⁴) ⁶ · i³ = 1 · (-1) = -1.

Luego la potencia de i con exponente "n" coincide con la potencia de i que tiene por exponente el resto de la división n entre 4.

   

5.- Calcula las potencias de i de exponentes: 25, 58, 243, -97, 164, -1545.

Observa cuál es su representación gráfica.
 
 

POTENCIA DE UN COMPLEJO EN FORMA BINÓMICA
 
 

Sea z = a+bi y n un número natural, teniendo en cuenta el desarrollo del binomio de Newton

 

 

 

 

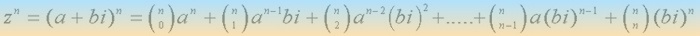
6.- Calcula en tu cuaderno y comprueba las siguientes potencias:

 

 

PRODUCTO DE UN NÚMERO COMPLEJO POR EL COMPLEJO i

   

Luego el vector que representa al complejo z·i se obtiene girando 90º en sentido positivo el vector que representa a z.

                       

 

 

 

 

 

 

 

7.- Modifica los parámetros de la escena anterior y observa que el ángulo formado por los vectores que representan a z y z·i siempre es de 90º.

 

RAIZ CUADRADA DE UN COMPLEJO EN FORMA BINÓMICA

 

La raíz cuadrada de un complejo z = a+bi es otro complejo x+yi tal que:

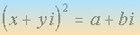
Resolviendo el sistema, obtenemos x e y.

 

8.- Calcula en tu cuaderno las raíces cuadradas de: 3+4i, -4+3i y 8-6i.

Comprueba los resultados utilizando la escena anterior.

 

 

 

 

 

 

Ir a forma polar

Ir a índice

 

Autor: Mª Ángeles Alonso González 

	© Ministerio de Educación, Cultura y Deporte. Año 2001