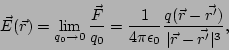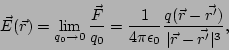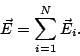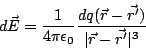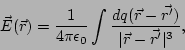Next: Líneas de Fuerza
Up: Electrodinámica
Previous: Ley de Coulomb y
El campo eléctrico es el intermediario en la interacción entre cargas eléctricas.
Cualquier definición del campo eléctrico tiene que permitir su cuantificación. Por ejemplo,
en la interacción entre dos cargas, una de ellas establece un campo eléctrico y la otra
interactú a con ese campo eléctrico. En consecuencia, tenemos dos problemas: 1) Determinar,
mediante medición o cálculo, el campo eléctrico establecido por una carga en cualquier
punto del espacio; 2) Calcular la fuerza que el campo ejerce sobre la otra carga ubicada
en cualquier punto del espacio.
Operacionalmente, definimos el campo eléctrico asociado a una colección de cargas
en términos de la fuerza ejercida sobre una carga de prueba positiva en un punto
determinado. Es importante que la carga de prueba sea lo suficientemente pequeña para
que no perturbe la distribución de cargas cuyo campo eléctrico setamos
tratando de medir. Esto es,
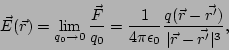 |
(4) |
donde 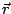 representa el vector posición del punto de observación y
representa el vector posición del punto de observación y 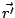 el vector posición
de la carga que produce el campo. Si el campo eléctrico es producido por un conjunto de
el vector posición
de la carga que produce el campo. Si el campo eléctrico es producido por un conjunto de 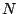 cargas
puntuales, el campo eléctrico total está dado por
cargas
puntuales, el campo eléctrico total está dado por
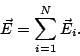 |
(5) |
Si el sistema de cargas es contínuo, el diferencial de campo eléctrico es
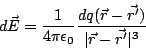 |
(6) |
y el campo eléctrico total en el punto de observación es
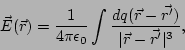 |
(7) |
donde 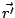 ahora representa el vector posición del elemento diferencial de carga. Observe
que la integración se realiza sobre la coordenada primada. Si la distribución es volumétrica
el
ahora representa el vector posición del elemento diferencial de carga. Observe
que la integración se realiza sobre la coordenada primada. Si la distribución es volumétrica
el 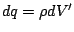 , donde
, donde 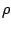 es la densidad volumétrica de carga. De igual forma, si la
distribución es superficial
es la densidad volumétrica de carga. De igual forma, si la
distribución es superficial 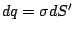 , o lineal
, o lineal
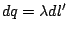 , donde
, donde 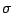 o
o 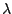 representan la densidad superficial de carga o la densidad lineal de carga.
representan la densidad superficial de carga o la densidad lineal de carga.



Next: Líneas de Fuerza
Up: Electrodinámica
Previous: Ley de Coulomb y
Willians Barreto
2006-10-06