


Next: Potencial Eléctrico
Up: Electrodinámica
Previous: Ley de Gauss
Ya en el estudio del dipolo eléctrico hicimos referencia a la energía potencial eléctrica,
siguiendo nuestra noción de energiía potencial y su relación con el trabajo realizado
para rotar el dipolo en contra del campo eléctrico externo. Aunque no lo comentamos anteriormente,
si el trabajo realizado por una fuerza sobre una partícula que se desplaza de una posición inicial a
otra final no depende de la trayectoria, entonces la fuerza es conservativa, como es el caso
de la fuerza eléctrica y la fuerza gravitacional. Cuando las fuerzas son conservativas, éstas
se pueden expresar a través de una función de energía potencial. Podemos asociar una energía
potencial a un sistema de tal forma que si colocamos una partícula cargada, ésta experimenta
una fuerza eléctrica. Así, la variación de energía potencial eléctrica cuando desplazamos
a una carga 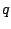 en presencia de un campo eléctrico externo
en presencia de un campo eléctrico externo 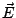 es
es
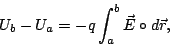 |
(13) |
donde la integral es independiente de la trayectoria entre los puntos 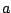 y
y 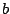 porque la fuerza
eléctrica es conservativa.
porque la fuerza
eléctrica es conservativa.
Ahora nos planteamos la siguiente pregunta:
¿Dónde reside la energía que un agente externo invierte cuando acerca (o aleja) dos cargas eléctricas?
Observemos que:
- Cargas de signos opuestos: Si dejamos una fija (
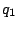 ) y alejamos la otra (
) y alejamos la otra (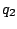 ), digamos hacia la derecha, se
realiza un trabajo negativo, resultando un incremento en la energía potencial. Si liberamos la
carga desde la separación mayor, debido a la atracción se acerca a la otra, disminuyendo la energía potencial
y aumentando la energía cinética.
), digamos hacia la derecha, se
realiza un trabajo negativo, resultando un incremento en la energía potencial. Si liberamos la
carga desde la separación mayor, debido a la atracción se acerca a la otra, disminuyendo la energía potencial
y aumentando la energía cinética.
- Cargas de signos iguales: Si desplazamos ahora la carga hacia la izquierda se produce un
aumento de la energía potencial. Al liberarla, la separación aumenta, decreciendo de nuevo la
anergía potencial y aumentando la energía cinética.
Independientemente del signo de las cargas
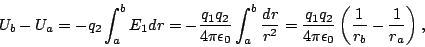 |
(14) |
Si 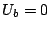 cuando
cuando
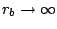
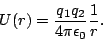 |
(15) |
Esta es la energía potencial eléctrica para un sistema conformado por dos cargas puntuales.
Para profundizar el concepto, supongamos que tres cargas puntuales se encuentran en el infinito:
- Traemos la carga
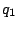 , ¿cuál es la energía potencial? Respuesta:
, ¿cuál es la energía potencial? Respuesta:
.
- Traemos la carga
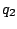 y hacemos la misma pregunta, respuesta:
y hacemos la misma pregunta, respuesta:
- Traemos la carga
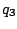 , respuesta:
, respuesta:
.
¿Nos estamos entendiendo? Este resultado es independiente del orden en que reunimos las cargas.
La energía que invierte un agente externo para reunir las tres cargas se almacena en el
campo eléctrico. Uhmmm, ¿Y por qué...?
Para un sistema de 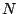 cargas puntuales tenemos
cargas puntuales tenemos
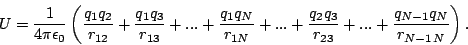 |
(16) |
Esto es una suma algebraica de escalares. Observe que 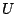 es una propiedad del sistema y no
de cargas individuales.
es una propiedad del sistema y no
de cargas individuales.
La energía potencial de un sistema de cargas fijas es igual al trabajo que debe
realizar un agente externo para reunir el sistema, desplazando cada carga una distancia
infinita.



Next: Potencial Eléctrico
Up: Electrodinámica
Previous: Ley de Gauss
Willians Barreto
2006-10-06
![]() cargas puntuales tenemos
cargas puntuales tenemos