Potencial Eléctrico

Definimos el potencial eléctrico como la energía potencial eléctrica por unidad de carga, así

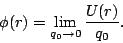$$\phi(r)=\lim_{q_0\rightarrow 0} \frac{U(r)}{q_0}.$$ (17)

El potencial puede ser negativo o positivo dependiendo del signo de la carga. La unidad internacional para el potencial eléctrico es el voltio: $[\phi]=V$.

Para una carga puntual el potencial es

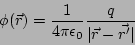$$\phi(\vec r)=\frac{1}{4\pi\epsilon_0}\frac{q}{\vert\vec r-\vec{r'}\vert}$$ (18)

y para una distribución continua de carga

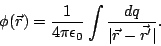$$\phi(\vec r)=\frac{1}{4\pi\epsilon_0}\int\frac{dq}{\vert\vec r-\vec{r'}\vert}.$$ (19)

Es posible determinar el campo elétrico si el potencial eléctrico es conocido. Veamos.

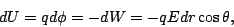$$dU=qd\phi=-dW=-qEdr\cos\theta,$$ (20)

esto es,

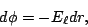$$d\phi=-E_\ell dr,$$ (21)

donde 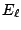$E_\ell$ es la componente del campo eléctrico paralela al desplazamiendo. Así,

$$E_\ell=-\frac{d\phi}{dr}.$$ (22)

Esto quiere decir que el campo eléctrico apunta en la dirección que disminuye el potencial. Si el potencial depende en general de las coordenadas rectangulares 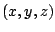$(x,y,z)$, entonces 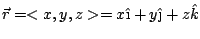$\vec r=<x,y,z>=x\hat{\i} + y\hat{\j} + z\hat k$ y podemos calcular las componentes rectangulares del campo eléctrico a través de

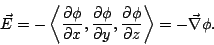$$\vec E=-\left<\frac{\partial\phi}{\partial x},\frac{\partial... ...l y},\frac{\partial\phi}{\partial z}\right>= -\vec\nabla \phi.$$ (23)