#include <tpl_graph.H>
 Inheritance diagram for Aleph::List_Graph< __Graph_Node, __Graph_Arc >:
Inheritance diagram for Aleph::List_Graph< __Graph_Node, __Graph_Arc >: Collaboration diagram for Aleph::List_Graph< __Graph_Node, __Graph_Arc >:
Collaboration diagram for Aleph::List_Graph< __Graph_Node, __Graph_Arc >:Classes | |
| struct | Arc_Iterator |
| class | Node_Arc_Iterator |
| struct | Node_Iterator |
Public Types | |
| using | GT = List_Graph |
| using | Node = __Graph_Node |
| The graph type. | |
| using | Arc = __Graph_Arc |
| The node class type. | |
| using | Node_Type = typename Node::Node_Type |
| The arc class type. More... | |
| using | Arc_Type = typename Arc::Arc_Type |
| The type of data stored in the arc. | |
| using | CommonBase = GraphCommon< List_Graph< __Graph_Node, __Graph_Arc >, __Graph_Node, __Graph_Arc > |
| using | Filter_Iterator = Digraph_Iterator< Filt > |
| using | In_Iterator = Digraph_Iterator< In_Filt > |
| using | Out_Iterator = Digraph_Iterator< Out_Filt > |
| using | ArcPair = tuple< __Graph_Arc *, __Graph_Node *> |
| Pair of arc and node (topologically related) | |
Public Member Functions | |
| virtual Node * | insert_node (Node *node) noexcept |
| virtual void | remove_node (Node *node) noexcept |
| Node * | get_first_node () const |
| Arc * | get_first_arc (Node *node) const |
| virtual void | remove_arc (Arc *arc) noexcept |
| virtual void | disconnect_arc (Arc *arc) noexcept |
| virtual Arc * | connect_arc (Arc *arc) noexcept |
| Arc * | get_first_arc () const |
| template<class Compare > | |
| void | sort_nodes (Compare &cmp) noexcept |
| template<class Compare > | |
| void | sort_nodes (Compare &&cmp=Compare()) noexcept |
| template<class Compare > | |
| void | sort_arcs (Compare &cmp) noexcept |
| template<class Compare > | |
| void | sort_arcs (Compare &&cmp=Compare()) noexcept |
| List_Graph (const List_Graph &g) | |
| List_Graph (List_Graph &&g) noexcept | |
| List_Graph & | operator= (const List_Graph &g) |
| List_Graph & | operator= (List_Graph &&g) noexcept |
| virtual | ~List_Graph () |
| Destructor: all the nodes and arcs and removed and freed. | |
| List_Graph () noexcept | |
| Construct an empty graph. | |
| void | swap (List_Graph &g) noexcept |
Swap in constant time this with g | |
| void *& | get_cookie () noexcept |
| Return a modifiable reference to graph's cookie. | |
| void * | get_cookie () const noexcept |
| Return a constant reference to graph's cookie. | |
| void *& | get_cookie (__Graph_Node *node) const noexcept |
Get a modifiable reference to the cookie pointer of node | |
| void *& | get_cookie (__Graph_Arc *arc) const noexcept |
Get a modifiable reference to the cookie pointer of arc | |
| bool | is_digraph () const noexcept |
Return true if the graph this is directed. | |
| void | set_digraph (bool val) |
| size_t | get_num_nodes () const noexcept |
| Return the total of nodes of graph. | |
| size_t | vsize () const noexcept |
| get_num_nodes() | |
| __Graph_Node * | get_node () const |
| __Graph_Node * | get_arc () const |
| __Graph_Node * | get_arc (__Graph_Node *p) |
| __Graph_Node * | get_src_node (__Graph_Arc *arc) const noexcept |
Return the source node of arc (only for directed graphs) | |
| __Graph_Node * | get_tgt_node (__Graph_Arc *arc) const noexcept |
Return the target node of arc (only for directed graphs) | |
| __Graph_Node * | get_connected_node (__Graph_Arc *arc, __Graph_Node *node) const noexcept |
| size_t | get_num_arcs () const noexcept |
| size_t | get_num_arcs (__Graph_Node *node) const noexcept |
| size_t | degree (__Graph_Node *p) const noexcept |
| size_t | esize () const noexcept |
| Return the total of arcs of graph. | |
| Bit_Fields & | get_control_bits (__Graph_Node *node) const noexcept |
Return a reference to control fields of node | |
| Bit_Fields & | get_control_bits (__Graph_Arc *arc) const noexcept |
Return a reference to the control bits of arc | |
| void | reset_bit (__Graph_Node *node, int bit) const noexcept |
Reset the bit of node (to zero) | |
| void | reset_bit (__Graph_Arc *arc, int bit) const noexcept |
Reset the bit of arc to zero. | |
| void | reset_bits (__Graph_Node *node) const noexcept |
Reset all the control bits of node | |
| void | reset_bits (__Graph_Arc *arc) const noexcept |
Reset all the control bits of arc | |
| int | get_bit (__Graph_Node *node, int bit) const noexcept |
Get the control bit of node | |
| int | get_bit (__Graph_Arc *arc, int bit) const noexcept |
Get the control bit of arc | |
| void | set_bit (__Graph_Node *node, int bit, int value) const noexcept |
Set the control bit of node to value | |
| void | set_bit (__Graph_Arc *arc, int bit, int value) const noexcept |
Set the control bit of arc to value | |
| long & | get_counter (__Graph_Node *node) const noexcept |
Get a modifiable reference to the counter of node | |
| long & | get_counter (__Graph_Arc *arc) const noexcept |
Get a modifiable reference to the counter of arc | |
| void | reset_counter (__Graph_Node *node) const noexcept |
Reset the node counter to zero. | |
| void | reset_counter (__Graph_Arc *arc) const noexcept |
Reset the acr counter to zero. | |
| void | reset_node_counters () const noexcept |
| Reset all the node counters of graph to zero. | |
| void | reset_node (__Graph_Node *p) const noexcept |
| void | reset_arc_counters () const noexcept |
| Reset all the arc counters of graph to zero. | |
| void | reset_arc (__Graph_Arc *arc) const noexcept |
| void | reset_nodes () const |
| void | reset_arcs () const |
| void | reset_bit_nodes (int bit) const noexcept |
Reset bit to zero for all the nodes of graph. | |
| void | reset_bit_nodes () const noexcept |
| Reset all the bits for all the nodes of graph. | |
| void | reset_bit_arcs (int bit) const noexcept |
Reset bit to zero for all the arcs of graph. | |
| void | reset_bit_arcs () const noexcept |
| Reset all the bits for all the arcs of graph. | |
| void | reset_counter_nodes () const noexcept |
| Reset all the counters to zero for all the nodes of graph. | |
| void | reset_counter_arcs () const noexcept |
| Reset all the counters to zero for all the arcs of graph. | |
| void | reset_cookie_nodes () const noexcept |
| void | reset_cookie_arcs () const noexcept |
| __Graph_Node * | insert_node (const Node_Type &node_info) |
| __Graph_Node * | insert_node (Node_Type &&node_info=Node_Type()) |
| __Graph_Node * | emplace_node (Args &&... args) |
| __Graph_Arc * | insert_arc (__Graph_Node *src, __Graph_Node *tgt, const Arc_Type &arc_info) |
| __Graph_Arc * | insert_arc (__Graph_Node *src, __Graph_Node *tgt, Arc_Type &&arc_info=Arc_Type()) |
| __Graph_Arc * | emplace_arc (__Graph_Node *src, __Graph_Node *tgt, Args &&... args) |
| bool | traverse_nodes (Operation &op) const noexcept(noexcept(op)) |
| bool | traverse_nodes (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | traverse_arcs (Operation &op) const noexcept(noexcept(op)) |
| bool | traverse_arcs (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | traverse_arcs (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| bool | traverse_arcs (__Graph_Node *p, Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | traverse_arcs (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| void | for_each_node (Operation &operation) const noexcept(noexcept(operation)) |
| void | for_each_node (Operation &&operation=Operation()) const |
| void | for_each_arc (Operation &op) const noexcept(noexcept(op)) |
| void | for_each_arc (Operation &&operation=Operation()) const |
| void | for_each_arc (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| void | for_each_arc (__Graph_Node *p, Operation &&op=Operation()) const noexcept(noexcept(op)) |
| for_each_arc(Node * p, Operation & operation) | |
| void | for_each_arc (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
Perform operation on each arc of node p | |
| bool | all_nodes (Operation &op) const noexcept(noexcept(op)) |
| bool | all_nodes (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | all_arcs (Operation &op) const noexcept(noexcept(op)) |
| bool | all_arcs (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | all_arcs (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| bool | all_arcs (__Graph_Node *p, Operation &&op=Operation()) const noexcept(noexcept(op)) |
| auto | nodes_map (std::function< T(__Graph_Node *)> op) const |
| auto | arcs_map (std::function< T(__Graph_Arc *)> operation) const |
| auto | arcs_map (__Graph_Node *p, std::function< T(__Graph_Arc *)> operation) const |
| T | foldl_nodes (const T &init, std::function< T(const T &, __Graph_Node *)> op) const |
| T | foldl_arcs (const T &init, std::function< T(const T &, __Graph_Arc *)> op) const |
| T | foldl_arcs (__Graph_Node *p, const T &init, std::function< T(const T &, __Graph_Arc *)> op) const |
| auto | filter_nodes (Op &op) const |
| auto | filter_nodes (Op &&op) const |
| auto | filter_arcs (Op &op) const |
| auto | filter_arcs (Op &&op) const |
| auto | filter_arcs (__Graph_Node *p, Op &op) const |
| auto | filter_arcs (__Graph_Node *p, Op &&op) const |
| bool | exists_node (Operation &op) const noexcept(noexcept(op)) |
| bool | exists_node (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | exists_arc (Operation &op) const noexcept(noexcept(op)) |
| bool | exists_arc (Operation &&op=Operation()) const noexcept(noexcept(op)) |
| bool | exists_arc (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| bool | exists_arc (__Graph_Node *p, Operation &&op=Operation()) const noexcept(noexcept(op)) |
| __Graph_Node * | search_node (Op &op) const noexcept(noexcept(op)) |
| __Graph_Node * | search_node (Op &&op) const noexcept(noexcept(op)) |
| __Graph_Node * | find_node (const Node_Type &info) const noexcept |
| __Graph_Arc * | search_arc (Op &op) const noexcept(noexcept(op)) |
| __Graph_Arc * | search_arc (Op &&op) const noexcept(noexcept(op)) |
| __Graph_Arc * | search_arc (__Graph_Node *p, Operation &op) const noexcept(noexcept(op)) |
| __Graph_Arc * | search_arc (__Graph_Node *p, Operation &&op=Operation()) const noexcept(noexcept(op)) |
| __Graph_Arc * | search_arc (__Graph_Node *src, __Graph_Node *tgt) const noexcept |
| __Graph_Arc * | find_arc (const Arc_Type &info) const noexcept |
| Container< __Graph_Node *> | nodes () const |
| Container< __Graph_Arc *> | arcs () const |
| Container< __Graph_Arc *> | arcs (__Graph_Node *p) const |
| auto | get_node_it () const noexcept |
| auto | get_arc_it () const noexcept |
| auto | get_arc_it (__Graph_Node *p) const noexcept |
| In_Iterator | get_in_it (__Graph_Node *p) const noexcept |
| Out_Iterator | get_out_it (__Graph_Node *p) const noexcept |
| __Graph_Arc * | search_directed_arc (__Graph_Node *src, __Graph_Node *tgt) const noexcept |
| DynList< __Graph_Node *> | in_nodes (__Graph_Node *p) const |
| DynList< __Graph_Node *> | out_nodes (__Graph_Node *p) const |
| DynList< __Graph_Arc *> | out_arcs (__Graph_Node *p) const |
| DynList< __Graph_Arc *> | in_arcs (__Graph_Node *p) const |
| auto | in_pairs (__Graph_Node *p) const |
| auto | out_pairs (__Graph_Node *p) const |
| size_t | in_degree (__Graph_Node *p) const noexcept |
| size_t | out_degree (__Graph_Node *p) const noexcept |
| bool | traverse_in_arcs (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| bool | traverse_in_arcs (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| void | for_each_in_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
Perform operation on each incoming arc of node p | |
| void | for_each_in_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| bool | all_in_arcs (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
Return true if op is true for all the incoming arcs to node p | |
| bool | all_in_arcs (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| bool | exists_in_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| bool | exists_in_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| auto | search_in_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| auto | search_in_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| auto | in_arcs_map (__Graph_Node *p, std::function< T(__Graph_Arc *)> op) const noexcept(noexcept(op)) |
| T | foldl_in_arcs (__Graph_Node *p, const T &init, std::function< T(const T &, __Graph_Arc *)> op) const noexcept(noexcept(op)) |
| DynList< __Graph_Arc *> | filter_in_arcs (__Graph_Node *p, Op &op) const |
| auto | filter_in_arcs (__Graph_Node *p, Op &&op=Op()) const |
| bool | traverse_out_arcs (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| bool | traverse_out_arcs (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| void | for_each_out_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
Perform operation on each incoming arc of node p | |
| void | for_each_out_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| bool | all_out_arcs (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
Return true if op is true for all the outcoming arcs to node p | |
| bool | all_out_arcs (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| bool | exists_out_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| bool | exists_out_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| auto | search_out_arc (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| auto | search_out_arc (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
| auto | out_arcs_map (__Graph_Node *p, std::function< T(__Graph_Arc *)> op) const |
| T | foldl_out_arcs (__Graph_Node *p, const T &init, std::function< T(const T &, __Graph_Arc *)> op) const noexcept(noexcept(op)) |
| DynList< __Graph_Arc *> | filter_out_arcs (__Graph_Node *p, Op &op) const noexcept(noexcept(op)) |
| auto | filter_out_arcs (__Graph_Node *p, Op &&op=Op()) const noexcept(noexcept(op)) |
Static Public Member Functions | |
| static void | map_nodes (N1 *p, N2 *q) noexcept |
| static void | map_arcs (A1 *p, A2 *q) noexcept |
Protected Member Functions | |
| void | init () noexcept |
| void | common_swap (List_Graph< __Graph_Node, __Graph_Arc > &g) noexcept |
Protected Attributes | |
| void * | cookie |
| size_t | num_nodes |
| size_t | num_arcs |
| bool | digraph |
Friends | |
| class | GraphCommon< List_Graph< __Graph_Node, __Graph_Arc >, __Graph_Node, __Graph_Arc > |
Graph implemented with double linked adjacency lists
This class manages two template parameters
__Graph_Node: the type of node, which previously must have been defined through of Graph_Node class.__Graph_Arc: the type of arc, which previously must have been defined through of Graph_Arc class.It is highly recommendable to use an alias for the final graph type. Some such as:
using My_Graph = List_Graph<Graph_Node<My_Node_Type>,
Graph_Arc<My_Arc_Type>>;
Once instantiated a List_Graph object, its nodes and arcs must be accessed through the following subclasses:
List_Graph<Node, Arc>::NodeList_Graph<Node, Arc>::ArcUsing of alias is very "natural". For the previous shown alias example, you could type:
My_Graph::Node * node_ptr = .... My_Graph::Arc * arc_ptr = ....
This graph can be directed or non directed. From a functional perspective, what gives the difference between a directed graph and a non-directed one, is the way for accessing to arcs given a node. Perhaps an example could help to understand better. Suppose that you have a graph g and two node pointers p and q respectively. Now, in order to specify an arc, you execute some such as:
auto arc = g.insert_arc(p, q);
If you execute
auto my_node = g.get_connected_arc(arc, p);
The you will get q, which is the node connected to p through arc. Now, if you execute
auto my_node = g.get_connected_arc(arc, q);
Then you will get p, which is the node connected to q through arc. In this situation you are trying g as a non-directed graph.
However, when you inserted the arc, you specified a source node and a target one. This knowledge, which is embedded in the internal data structure, can be profited by the user for treating g as a directed graph. In that case, instead of using the get_connected_node() method, you use other methods expressing the arc sense. For instance, in the previous example you could do:
auto src = g.get_src_node(arc); // source node of arc auto tgt = g.get_tgt_node(arc); // target node of arc
List_Digraph Aleph-w ( 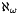 ) exports a derived named
) exports a derived named List_Digraph. At the functional level, there is no almost any difference with List_Graph. The only functional difference is that get_connected_node() has no any sense on List_Digraph objects. Be very careful with the fact that Aleph-w ( 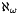 ) does not perform any check of this. To use
) does not perform any check of this. To use get_connected_node() for List_Digraph objects is an programming error.
So that, if there is no practically much difference, then, why to use List_Digraph?
Probably List_Graph is the more versatile graph class of Aleph-w ( 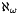 ). However, its versatility is at the expense of highest memory consumption. First, the internal lists are double, not single. Second, for each arc, there is a double linked list of arc references. This implicates that the same arc information is duplicated in each involved node, the source and the target one.
). However, its versatility is at the expense of highest memory consumption. First, the internal lists are double, not single. Second, for each arc, there is a double linked list of arc references. This implicates that the same arc information is duplicated in each involved node, the source and the target one.
At the contrary, in List_Digraph the arc references are not stored in the target node. This fact could considerably save memory.
For List_Graph all (yes, all!) operations are 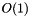 , but, as said, this performane is achieved at the expense of memory.
, but, as said, this performane is achieved at the expense of memory.
For List_Digraph all operations are 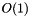 , except node removal. In this case, since with this representation there is no direct way for knowing the incoming arcs, the node removal requires to traverse all the arcs for checking for those incoming to the removed one. So, the node removal is
, except node removal. In this case, since with this representation there is no direct way for knowing the incoming arcs, the node removal requires to traverse all the arcs for checking for those incoming to the removed one. So, the node removal is  .
.
List_Graph vs List_Digraph) So that, a guideline for choosing List_Graph vs List_Digraph is to ask if the node removal will be used. If yes, then how often? If you know that the node removal will be used several times, then prefer List_Graph; otherwise, that is, you know there is no node removals, then use List_Digraph, since it uses less memory.
Almost all the methods of this class do not perform any validation. This is especially delicate for those methods involved topologic changes (insertions and removals of nodes or arcs).
When an removal operation is called, this assumes that it is performed on a valid object. For example, remove_node(p) assumes that p is a valid node pointer. For valid we understand that the pointer was returned for another method of graph class and on the same graph. At this regard, is very important to be careful because no method validates if the involved object was or not created neither this belongs to the graph.
|
inherited |
Alias for Digraph_Iterator
|
inherited |
Iterator on incoming arcs of node
| using Aleph::List_Graph< __Graph_Node, __Graph_Arc >::Node_Type = typename Node::Node_Type |
The arc class type.
The type of data stored in the node
|
inherited |
Iterator on incoming arcs of node
|
inline |
Copy constructor.
Build a new graph with a copy of graph g. Al the data content for the nodes and arc are copied to the new graph, what requires that the copy constructors and copy assignment for each data type (of node and the arc) are defined.
The new graph is completely isomorphic to g.
| [in] | g | graph to be copied |
| bad_alloc | bad_alloc if there is no enough memory |
|
inlinenoexcept |
Construct a new graph by moving a graph g.
This construction is 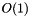 because no copy is done; simply
because no copy is done; simply g is moved to the new graph. After construction, g becomes empty, what it is not a problem beceause it is sure that g is a rvalue (it is temporal).
| [in] | g | graph to be moved |
|
inlinenoexceptinherited |
Check if all the arcs of graph satisfy a boolean condition.
all_arcs() traverse each arc of graph and on each one the operation is tested. If operation returns true, then the next arc is inspected. Otherwise, the traversal stops and false is returned as result.
The operation must imperatively have the following structure:
bool operation(Arc * p)
The idea is to perform a test and according to its result to return true is the test was passed, or false otherwise. For example, in order to check if all the arc content is odd you could do:
g.all_arcs([] (auto a) { return a->get_info() % 2; });
all_arcs() is semantically equivalent to traverse_arcs().The complexity for this primitive always is  worst case.
worst case.
| [in] | operation | condition to test on each arc. |
true if all the arcs satisfy the condition; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Check if all the arcs adjacent to a node satisfy an boolean condition.
all_arcs(p) traverse each arc adjacent to node p and on each one the operation is tested. If operation returns true, then the next arc is inspected. Otherwise, the traversal stops and false is returned as result.
The operation must imperatively have the following structure:
bool operation(Arc * p)
The idea is to perform a test and according to its result to return true is the test was passed, or false otherwise. For example, in order to check if all the arc content is odd you could do:
g.all_arcs(p, [] (auto a) { return a->get_info() % 2; });
all_arcs(p) is semantically equivalent to traverse_arcs().The complexity for this primitive always is 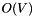 worst case for dense graphs.
worst case for dense graphs.
| [in] | p | node pointer |
| [in] | operation | condition to test on each arc. |
true if all the arcs satisfy the condition; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Check if all the nodes of graph satisfy an boolean condition.
all_nodes() traverse each node of graph and on each one operation is tested. If operation returns true, then the next node is inspected. Otherwise, the traversal stops and false is returned as result.
The operation must imperatively have the following structure:
bool operation(Node * p)
The idea is to perform a test and according to its result to return true is the test was passed, or false otherwise. For example, in order to check if all the nodes content is even you could do:
g.all_nodes([] (auto p) { return p->get_info() % 2 == 0; });
all_nodes() is semantically equivalent to traverse_nodes().The complexity for this primitive always is 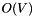 worst case.
worst case.
| [in] | operation | condition to test on each node. |
true if all the nodes satisfy the condition; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Return a container with all the arcs of the graph.
arcs() recollects all the arcs of the graph and builds a container with all them inserted. The container type is a template parameter, which by default is DynList.
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Return a container with all the arcs adjacent to a node.
arcs() recollects all the arcs adjacent to node p and builds a container with all them inserted. The container type is a template parameter, which by default is DynList.
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Map the arcs of a graph to a specific range.
arcs_map(operation) produces a mapping list of the graph's arcs. The transformation is done by operation whose signature must imperatively be:
T operation(Arc * a)
operation instruments a map from the arc to the range type T. By default, T is Arc_Type (the type associated to the arc's data). In this case, you do not require to specify the range type as template parameter. Otherwise, in order to the compiler can know the range type, you must specify it as template parameter.
Suppose by example that the arcs have integers and that you want to produce a mapping int –> string corresponding to string reprsentation of the data arc. Then you can do this as follows:
auto l = g.map_arcs<string>([] (auto a)
{
return to_string(a->get_info());
});
arcs_map() instead of map_arcs()) is due to the ambiguity that would cause with the map_arcs() intended for mapping the arcs through their cookies.template keyword before the name arcs_map<your-target-type>. g.template arcs_map<ulong>([] (auto p) { return p->get_info(); });
| [in] | operation | transformation from ARc* to T to be performed on each arc. |
DynList<T> containing the mapping. | bad_alloc | if there is no enough memory for fuilding the dynamic list or anything else that can throw operation |
|
inlineinherited |
Map the adjacent arcs of a node to a specific range.
arcs_map(p, operation) produces a mapping list of the arcs adjacent to node p. The transformation is done by operation whose signature must imperatively be:
T operation(Arc * a)
operation instruments a map from the arc to the range type T. By default, T is Arc_Type (the type associated to the arc's data). In this case, you do not require to specify the range type as template parameter. Otherwise, in order to compiler can know the range type, you must specify it as template parameter.
Suppose by example that the arcs have doubles and that you want to produce a mapping double –>  . Then you can do this as follows:
. Then you can do this as follows:
auto l = g.map_arcs([] (auto a) { return sqrt(a->get_info()); });
Since the return type is the same than the arc content, it would not be necessary to pass a template parameter indicating the range type. If this was not be the situation, then you would have to specify the range type as template parameter.
arcs_map() instead of map_arcs()) is due to the ambiguity that would cause with the map_arcs() intended for mapping the arcs through their cookies.template keyword before the name arcs_map<your-target-type>. g.template arcs_map<ulong>([] (auto p) { return p->get_info(); });
| [in] | operation | transformation from Arc* to T to be performed on each arc. |
DynList<T> containing the mapping. | bad_alloc | if there is no enough memory for fuilding the dynamic list or anything else that can throw operation |
|
inlinevirtualnoexcept |
Connect an previously disconnected arc to the graph.
This method serves for connecting an arc that has been disconnected with disconnect_arc() method. Once connected, the arc is again part of the graph and can be removed and freed by remove_arc() or by the destructor.
| [in] | arc | pointer to the arc to connect |
|
inlinenoexceptinherited |
Return the total of arcs (or degree) of a node. Only has sense for non directed graphs
|
inlinevirtualnoexcept |
Disconnect an arc from graph.
This method removes an arc from the graph; that is, it does not longer belong to the graph. However, the memory is not freed.
Although the use of this method is occasional, it not exceptional. For example, some situations require temporarily disconnect the arc and afterward connect it again.
The disconnected arc is already for beeing reinserted in the graph with the connect_arc() method.
remove_arc(). In fact, to call remove_arc() on a disconnected arc is an error. It is your responsability to free an disconnected arc.| [in] | arc | pointer to the arc to disconnect |
|
inlineinherited |
Insert a new arc in the graph by constructing its associated data in-place with the given args.
This method allows to insert a new arc in the graph bypassing innecesary copies. emplace_arc() allocates a new arc, takes the parameters received and calls to the constructor of data associated to the arc. Then the data is forwarded to the arc data constructor avoiding, if possible, innecessary copies. Once the arc is completely built, this is inserted, at this moment without any logic possibility of failure, into the graph.
| [in] | src | pointer to the source node. |
| [in] | tgt | pointer to the target node. |
| [in] | args | variadic argument list for the construction of data associated to the arc. |
| bad_allod | if there is no enough memory. |
|
inlineinherited |
Insert a new node in the graph by constructing it in-place with the given args.
This method is an effective way for inserting a new node in the graph and bypassing innecesary copies. emplace_node() allocates a new node, takes the parameters received and calls to the constructor of data associated to the node. Then the data is forwarded to the node data constructor avoiding, if possible, innecessary copy. Once the node is completely built, this is inserted, at this moment without any logic possibility of failure, into the graph.
| [in] | args | variadic argument list for the construction of data associated to the node. |
| bad_allod | if there is no enough memory. |
|
inlinenoexceptinherited |
Determine if exists at least a arc satisfying a condition.
exists_arc(op) returns true if at least a node of graph satisfies the condition expressed by operation.
The operation has  complexity for the worst case.
complexity for the worst case.
exists_arc() is the oppossite or complement of all_arcs(). In fact, exists_arc(op) could be written, in terms of all_arc(op) as follows: not g.all_arc([&op] (auto p) { return not op(p); });
| [in] | operation | for testing existing condition |
true if at least a node satisfaying the condition is found; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Determine if exists at least a arc adjacent to a node satisfying a condition.
exists_arc(p, op) returns true if at least a node adjacent to p satisfies the condition expressed by operation.
The operation has 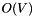 complexity for the worst case; concretely on dense graphs, but it trends to be much lesser for sparsed graphs.
complexity for the worst case; concretely on dense graphs, but it trends to be much lesser for sparsed graphs.
exists_arc() is the oppossite or complement of all_arcs(). In fact, exists_arc(p, op) could be written, in terms of all_arc(p, op) as follows: not g.all_arc(p, [&op] (auto p) { return not op(p); });
| [in] | p | node from which you want to access its arcs |
| [in] | operation | for testing existing condition |
true if at least a node satisfaying the condition is found; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Return true if it exists a incoming arc to p returning true for op
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Determine if exists at least a node satisfying a condition.
exists_node(op) returns true if at least a node of graph satisfies the condition expressed by operation.
The operation has 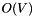 complexity for the worst case.
complexity for the worst case.
exists_node() is the oppossite or complement of all_nodes(). In fact, exists_node(op) could be written, in terms of all_nodes(op) as follows: not g.all_nodes([&op] (auto p) { return not op(p); });
| [in] | operation | for testing existing condition |
true if at least a node satisfaying the condition is found; false otherwise.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Return true if it exists a outcoming arc to p returning true for op
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Filter the arcs of graph satisfying a condition.
filter_arcs(op) traverses each arc of graph and recolects those satisfying the condition expressed by op. op must match the following signature:
bool op(Arc * a)
If op(p) returns true, then a is filtered (recollected) towards a final dynamic list containing the filtered arcs.
For example, if the arcs contain integers, then the following code snippet recollects those nodes whose value is greater than x:
g.filter_arcs([x] (auto a) { return a->get_info() > x; });
| [in] | op | operation implementing the filtering condition. |
| bad_alloc | if there is no enough memory for building the full returning list. |
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Filter the arcs adjacent to a node satisfying a condition.
filter_arcs(p, op) traverses each arc adjacent to node p and recolects those satisfying the condition expressed by op. op must match the following signature:
bool op(Arc * a)
If op(p) returns true, then a is filtered (recollected) towards a final dynamic list containing the filtered arcs.
For example, in order to get the arcs whose target node have degree greater than n you could do it as follows:
g.filter_arcs(p, [&g, p, n] (auto a)
{
return g.degree(g.get_connected_node(a, p)) > n;
});
Note the closure (or captured) data: the graph g, by reference in order to avoid copying it, the pointer p to te source node and the value of n.
| [in] | p | pointer to node wanted to explore and to filter its adjacent arcs. |
| [in] | op | operation implementing the filtering condition. |
| bad_alloc | if there is no enough memory for building the full returning list. |
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Filter the incoming arcs of a node.
This method is analogous to filter_arcs() but only operates on the incoming arcs.
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Filter the nodes satisfying a condition.
filter_nodes(op) traverses each node of graph and recolects those satisfying the condition expressed by op. op must match the following signature:
bool op(Node * p)
If op(p) returns true, then p is filtered (recollected) towards a final dynamic list containing the filtered nodes.
For example, if the nodes contain integer, then the following code snippet recollects those nodes whose value is greater than x:
g.filter_nodes([x] (auto p) { return p->get_info() > x; });
| [in] | op | operation implementing the filtering condition. |
| bad_alloc | if there is no enough memory for building the full returning list. |
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Filter the outcoming arcs of a node.
This method is analogous to filter_arcs() but only operates on the outcoming arcs.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Find an arc mathing a content.
find_arc(info), which is a wrapper to search_arc(), searches a arc whose get_info() result matches with the info parameter. The comparison is done via de operator == on the class Arc_Type, which is usually the case.
| [in] | info | to be compared with arcs content |
info or nullptr otherwise.
|
inlinenoexceptinherited |
Find a node mathing a content.
find_node(info), which is a wrapper to search_node(), search a nodo whose get_info() result matches with the info parameter. The comparison is done via de operator == on the class Node_Type, which is usually the case.
| [in] | info | to be compared with nodes content |
info or nullptr otherwise.
|
inlineinherited |
Folding of arcs on a graph.
foldl_arcs(init, operation) traverse all arc of graph and maintain an accumulator value acc whose initial value is init. On each acr a, it performs operation(acu, a) which must match with the following signature:
T operation(const T &, Arc * a)
So, on each call it is peformed:
acc = operation(acc, a);
Therefore acc serve as an accumulator.
Since foldl_arcs() is defined via std::function wrapper, it is very important to match the expected signature of operation. A proper and sure way of quickly define operation is by using auto parameters.
For example, suppose that the arcs contain doubles and that you want to compute the total sum, then you could do it as follows:
g.foldl_arcs(p, [] (auto acc, auto node)
{
return acc + arc->get_info();
});
| [in] | init | initial value of accumulator |
| [in] | operation | to be performed, which must match the signature previously explained. |
|
inlineinherited |
Folding of arcs of a node.
foldl_arcs(p, init, operation) traverse all the arcs adjacent to node p and maintain an accumulator value acc whose initial value is init. On each arc a, it performs operation(acu, a) which must match with the following signature:
T operation(const T &, Arc * a)
So, on each call it is peformed:
acc = operation(acc, a);
Therefore acc serves as an accumulator.
Since foldl_arcs() is defined via std::function wrapper, it is very important to match the expected signature of operation. A proper and sure way of quickly define operation is by using auto parameters.
For example, suppose that the arcs contain doubles and that you want to compute the total sum, then you could do it as follows:
g.foldl_arcs(p, [] (auto acc, auto node)
{
return acc + arc->get_info();
});
| [in] | p | node from where to access its adjacent arcs |
| [in] | init | initial value of accumulator |
| [in] | operation | to be performed, which must match the signature previously explained. |
|
inlinenoexceptinherited |
Fold the incoming arcs of a node.
This method is analogous to foldl_arcs() but only operates on the incoming arcs.
|
inlineinherited |
Folding of nodes on a graph.
foldl_nodes(init, operation) traverse all node of graph and maintain an accumulator value acc whose initial value is init. On each node p, it performs operation(acu, p) which must match with the following signature:
T operation(const T &, Node * p)
So, on each call it is peformed:
acc = operation(acc, p);
Therefore acc serve as an accumulator.
Since foldl_nodes() is defined via std::function wrapper, it is very important to match the expected signature of operation. A proper and sure way of quickly define operation is by using auto parameters.
For example, suppose that the nodes contain integers and that you want to compute the maximum value. Then you could do it as follows:
g.foldl_nodes(numeric_limits<int>::min(), [] (auto acc, auto node)
{
return max(acc, node->get_info();
});
| [in] | init | initial value of accumulator |
| [in] | operation | to be performed, which must match the signature previously explained. |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Unconditionally traverse all the arcs of graph and on each one perform an operation.
for_each_arc() unconditionally traverse all the arcs of a graph and on each one performs operation, which must have the following signature:
void operation(Arc * p)
The operation could be a function pointer matching that signature, a functor or a lambda. Note that the operation does not require return anything.
Your algorithm should not assume any particular order of visit.
If your goal is to initialize control state of the arcs, then don't use this method. Instead, use reset_arcs() or their derivatives according your situation.
The complexity for this primitive always is  .
.
| [in] | operation | to be performed on each node. |
| anything | that can throw operation. |
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Unconditionally traverse all the arcs adjacnt to a node and on each one perform an operation.
for_each_ars(p) unconditionally traverse all the nodes of node p on each one performs operation, which must have the following signature:
void operation(Arc * p)
The operation could be a function pointer matching that signature, a functor or a lambda. Note that the operation does not require return anything.
This probably is the most common primitive for algorithms on graphs.
The complexity for this primitive always is 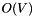 worst case, but on sparsed graphs a fraction of
worst case, but on sparsed graphs a fraction of  or better
or better 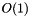 for special buy common graphs such as "small word" networks.
for special buy common graphs such as "small word" networks.
Your algorithm should not assume any particular order of visit.
p. If you want to know the node connected to p then invoke to g.get_connected_node(a,p).for_each_in_arc() or for_each_out_arc()-
|
inlinenoexceptinherited |
Unconditionally traverse all the nodes of graph and on each one perform an operation.
for_each_node() unconditionally traverse all the nodes of a graph and on each one performs operation, whicsh must have the following signature:
void operation(Node * p)
The operation could be a function pointer matching that signature, a functor or a lambda. Note that the operation does not require return anything.
Your algorithm should not assume any particular order of visit.
If your goal is to initialize control state of the nodes, then don't use this method. Instead, use reset_nodes() or their derivatives according your situation.
The complexity for this primitive always is 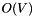 .
.
| [in] | operation | to be performed on each node. |
| anything | that can throw operation. |
|
inlineinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Return any arc in the graph.
This method serves as an depart arc in the graph. Some algorithms only need an initial arc which could be anyone. In these cases, this method is indicated.
|
inlineinherited |
Return any arc adjacent to a node.
This method serves as an arc of depart given a node. Some algorithms only need any arc adjacent to a node in order to start their computations. In these cases, this method is indicated.
p
|
inlinenoexceptinherited |
Obtains an iterator to the arc of graph.
This method is useful for shorting the iterator initialization. A traditional way for writing an iterator is as follows:
for (typename GT::Arc_Iterator it(g); it.has_curr(); it.next()) operation on current arc
With get_arc_it() The previous snippet could be more shortly written thus:
for (auto it = g.get_arc_it(); it.has_curr(); it.next()) operation on current arc
|
inlinenoexceptinherited |
Obtains an iterator to the adjacent arcs of a node.
This method is useful for shorting the iterator initialization. A traditional way for writing an iterator on the arcs of a node is as follows:
for (typename GT::Node_Arc_Iterator it(g); it.has_curr(); it.next()) operation on current arc
With get_arc_it(p) The previous snippet could be more shortly written thus:
for (auto it = g.get_arc_it(p); it.has_curr(); it.next()) operation on current arc
|
inlinenoexceptinherited |
Return the adjacent node to node through arc.
This method only has sense for non-directed graphs. In fact, for non directed graphs, this is the proper way for accessing to a target node from a specific arc.
This is the expected way for accesing the adjacent nodes to a specific node. From a node p, we can see its arcs through a iterator of a funcrional for_each().
As example, consider the following code snippet which examinates the adjacent nodes from a node p:
for (auto it = g.get_arc_it(p); it.has_curr(); it.next())
{
auto arc = it.get_curr(); // obtain the current arc
auto tgt = g.get_connected_node(arc, p); // the adjacent node
... }
| [in] | arc | the arc |
| [in] | node | the node from you must be seeing the arc |
p ---arc--- tgt
|
inline |
Return any arc adjacent to a node.
This method serves as an arc of depart given a node. Some algorithms only need any arc adjacent to a node in order to start their computations. In these cases, this method is indicated.
node
|
inline |
Return any arc in the graph.
This method serves as an arc of depart in the graph. Some algorithms only need an initial arc which could be anyone. In these cases, this method is indicated.
|
inline |
Return any node in the graph.
This method serves as an entry point to the graph. Some algorithms only need an initial node which could be anyone. In these cases, this method is indicated.
|
inlinenoexceptinherited |
Return an input iterator on the incoming arcs to p
This method is useful for shorting an input iterator initialization. A traditional way for writing an input iterator on the arcs of a node is as follows:
for (typename GT::In_Iterator it(g); it.has_curr(); it.next()) operation on current arc
With get_in_it(p) The previous snippet could be more shortly written thus:
for (auto it = g.get_in_it(p); it.has_curr(); it.next()) operation on current arc
|
inlineinherited |
Return any node in the graph.
This method serves as an entry point to the graph. Some algorithms only need an initial node which could be anyone. In these cases, this method is indicated.
|
inlinenoexceptinherited |
Obtains an iterator to the nodes of graph.
This method is useful for shorting the iterator initialization. A traditional way for writing an iterator is as follows:
for (typename GT::Node_Iterator it(g); it.has_curr(); it.next()) operation on current node
With get_node_it() The previous snippet could be more shortly written thus:
for (auto it = g.get_node_it(); it.has_curr(); it.next()) operation on current node
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Return the total of arcs of a node. Only has sense for non directed graphs
|
inlinenoexceptinherited |
Return an output iterator on the incoming nodes to p
This method is useful for shorting an output iterator initialization. A traditional way for writing an output iterator on the arcs of a node is as follows:
for (typename GT::Out_Iterator it(g); it.has_curr(); it.next()) operation on current arc
With get_out_it(p) The previous snippet could be more shortly written thus:
for (auto it = g.get_out_it(p); it.has_curr(); it.next()) operation on current arc
|
inlineinherited |
Return a list with the incoming arcs to p`
The method returns all the incoming arcs s --> p.
| bad_alloc | if there is no enough memory |
|
inlinenoexceptinherited |
Return a list of incoming arcs of a node mapped to items of type given by transformation op.
This method is analogous to arcs_map() but only operates on the incoming arcs.
|
inlinenoexceptinherited |
Compute the input degree of a node.
The method computes, not retrieves, the number of incoming arcs to node p. Be careful with the fact that this is a computation and to perform very often could degrade the performance.
Note that this method does not only serve too for explicit digraphs, but that would be necessary, since the in degree is neves stored.
| [in] | p | poinger to the node |
p
|
inlineinherited |
Return a list with the incoming nodes to p
The method filters all the incoming arcs s --> p and return their nodes.
| [in] | p | pointer to node |
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Return a list of pair incoming arcs and nodes.
Sometimes is useful to directly have the incoming arcs and their nodes. This method perform that task in only a pass.
The pair are implemented with tuples. First item has the arc and the second the node.
| [in] | p | pointer to node |
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Create and insert a new arc linking two nodes and copying data.
insert_arc() allocates a new arc linking the nodes pointed by src and tgt. If this is a directed graph, then src is considered the source node and tgt the target one. When the arc has been effectively allocated, the data contained in arc_info is copied to the node. Finally, the arc is inserted into the graph.
The pointers srcand tgt must be valid; that is, of course, they must correspond to real nodes already inserted in the graph. At this regard, no validation is done.
| [in] | src | pointer to the source node. |
| [in] | tgt | pointer to the target node. |
| [in] | arc_info | the data to be copied to the node. |
| bad_alloc | if there is no enough memory. |
|
inlineinherited |
Create and insert a new arc linking two nodes and moving the received data.
Thi method firstallocates a new arc linking the nodes pointed by srcandtgt. Ifthisis a directed graph, thensrcis considered the source node andtgt` the target one. Once the arc has been effectively allocated, if possible, the data contained in arc_info is moved to the node avoiding copy. Finally, the arc is inserted into the graph.
The pointers srcand tgt must be valid; that is, of course, they must correspond to real nodes already inserted in the graph. At this regard, no validation is done.
| [in] | src | pointer to the source node. |
| [in] | tgt | pointer to the target node. |
| [in] | arc_info | the data to be moved to the node. |
| bad_alloc | if there is no enough memory. |
|
inlinevirtualnoexcept |
Insertion of a node already allocated.
This methods takes a pointer to a node already allocated and inserts it in the graph.
The node allocation and its live in memory is user's responsability. At this regard, take in account that the graph destructor and remove_method() will assume that the nodes were allocated with new operator and consequently it will call to delete for deallocating. So, it is very dangerous to use nodes whose memory does not come from new.
remove_noe() will call to delete operator, it is preferable and highly recommended to use any other overloaded version of insert_node() which automatically allocates node's memory. In fact, those overloaded methods invoke this version.| [in] | node | a pointer to an already allocated node. |
|
inlineinherited |
Allocate a new node, set by copy its data content and insert it into the graph.
This method perform several actions. First, it allocates memory for a graph node. Then the data node_info is copied to the data associated to the node. This copy is done via the copy constructor and assign operator. So, these functionalities must be present for the class Node_Type. Finally, the node is topologically inserted into the graph.
| [in] | node_info | infopr to copy to the new node. The copy constructor and the assign operator must be defined for the class Node_Type. |
| bad_allod | if there is no enough memory |
|
inlineinherited |
Allocate a new node, set by moving its data content and insert it into the graph.
This method perform several actions. First, it allocates memory for a graph node. Then the data node_info is moved to the data associated to the node. This movement is done via the move constructor and move assign operator. So, these functionalities must be present for the class Node_Type. Finally, the node is topologically inserted into the graph.
| [in] | node_info | info to move to the new node. The move constructor and the move assign operator must be defined for the class Node_Type. |
| bad_allod | if there is no enough memory. |
|
inlinestaticnoexceptinherited |
Map the arcs through their cookies.
map_arcs(p, q) is intended to biyectively to map the arc p towards the arc q through their cookies. Basically, after calling the cookie of p points to q and the cookie of q points to p.
See map_nodes() for a better explanation.
| [in] | p | source arc of mapping |
| [in] | q | target arc of mapping |
|
inlinestaticnoexceptinherited |
Map the nodes through their cookies.
map_nodes(p, q) is intended to biyectively to map the node p towards the node q through their cookies. Basically, after calling the cookie of p points to q and the cookie of q points to p.
If the cookie value of p is not nullptr, then map_nodes(p, q) assumes that there already is a mapping and then perform the composition. This could be very useful for having several mapping.
Supposse that we have three nodes p, q and r belonging to three different, but from certain way isomorphic, graphs g1 and g2 of type GT, and g3 of type GTT. Note that the types of graph could variate. Thus, this call:
g1.map_nodes(p, q);
Instruments a biyective mapping  . Note that since
. Note that since p and q are of the same type (although belong to different graphs), it is not necessary to specify as template parameters the graph types. Another way for invoking exactly the same function is:
GT::map_nodes(p, q);
This is because map_nodes() is a static member.
Now, suppose that you wish to map the node r to p and q- Ypu could do as follows:
g1.map_nodes<GT, GTT>(p, r);
Now the mapping is  . Note that in this case, since the graph types are not the same, you must specify them as template parameters. Of course, in this case, for retrieving
. Note that in this case, since the graph types are not the same, you must specify them as template parameters. Of course, in this case, for retrieving r you must do two cookie's inspections, one first on p for retrieving q, and a second on q for retrieving r.
In our experiences, this is the fastest way for implementing mappings. Apart from the fact that the retrieval is 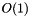 , this is also deterministic. Compare this fact with other approaches requiring bookkeeping throug hash tables or trees. In addiction, if many (or all) nodes are required to map, then this approach is also the less space consuming. More still, correctly used, this approach could be simpler than hash tables or trees, since you do not require additional declarations, inicializations, etc.
, this is also deterministic. Compare this fact with other approaches requiring bookkeeping throug hash tables or trees. In addiction, if many (or all) nodes are required to map, then this approach is also the less space consuming. More still, correctly used, this approach could be simpler than hash tables or trees, since you do not require additional declarations, inicializations, etc.
Of course, this approach has the big con that it is not very typed neither validated. If you do a mistake all probably will crash. However, the big gain in speed rewards and deserves the presence of this feature.
| [in] | p | source node of mapping |
| [in] | q | target node of mapping |
|
inlineinherited |
Return a container with all the nodes of the graph.
nodes() recollects all the nodes of the graph and builds a container with all them inserted. The container type is a template parameter, which by default is DynList.
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Map the nodes of a graph to a specific range.
nodes_map(operation) produces a mapping list of the graph's nodes. The transformation is done by operation whose signature must imperatively be:
T operation(Node * p)
operation instruments a map from the node to the range type T. By default, T is Node_Type (the type associated to the node's data). In this case, you do not require to specify the range type as template parameter. Otherwise, in order to the compiler can know the range type, you must specify it as template parameter.
Suppose by example that the nodes have integers and that you want to produce a mapping int –> double corresponding to the division of the data node between a specific divisor. Then you can do this as follows:
auto l = g.map_nodes<double>([divisor] (auto p)
{
return 1.0*p->get_info()/divisor;
});
nodes_map() instead of map_nodes()) is due to the ambiguity that would cause with the map_nodes() intended for mapping the nodes through their cookies.template keyword before the name nodes_map<your-target-type>. g.template nodes_map<ulong>([] (auto p) { return p->get_info(); });
| [in] | operation | transformation from Node* to T to be performed on each node. |
DynList<T> containing the mapping. | bad_alloc | if there is no enough memory for fuilding the dynamic list or anything else that can throw operation |
|
inline |
Assign by copy g to this.
This operator removes and frees all the nodes and arcs of this and then copy g.
| [in] | g | graph to copy |
| bad_alloc | if there is no enough memory |
|
inlinenoexcept |
Assign by moving g to this.
This assignment moves in constant time all g content to this.
| [in] | g | graph to copy |
|
inlineinherited |
Return a list with the outcoming arcs to p`
The method returns all the outcoming arcs p --> t.
| [in] | p | pointer to node |
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Return a list of outcoming arcs of a node mapped to items of type given by transformation op.
This method is analogous to arcs_map() but only operates on the outcoming arcs.
|
inlinenoexceptinherited |
Compute the output degree of a node.
The method computes, not retrieves, the number of outcoming arcs to node p. Be careful with the fact that this is a computation and to perform very often could degrade the performance.
Note that if you are using a digraph, then it is not use to have this method, since the digraph stores the outcoming degree. In this case, you could use get_num_arcs(p) in order to obtain the same result wihout any computation
| [in] | p | poinger to the node |
p
|
inlineinherited |
Return a list with the outcoming nodes to p
The method filters all the outcoming arcs p --> t and return their nodes.
| [in] | p | pointer to node |
| bad_alloc | if there is no enough memory |
|
inlineinherited |
Return a list of pair outcoming arcs and nodes.
Sometimes is useful to directly have the outcoming arcs and their nodes. This method perform that task in only a pass.
The pair are implemented with tuples. First item has the arc and the second the node.
| [in] | p | pointer to node |
| bad_alloc | if there is no enough memory |
|
inlinevirtualnoexcept |
Remove an arc from the graph and free it.
| [in] | pointer | to the arc to be removed from graph and free it |
|
inlinevirtualnoexcept |
Remove a node from the graph and free its memory.
This method removes all the incoming and outcoming arcs referred to the node and frees the memory. Then removes the node from graph and frees its memory. All the memory occuped by the arcs related to the node and the node itselg is freed.
The methods takes 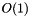 on
on List_Graph objects and  on
on List_Digraph objects**.
| [in] | node | to be removed and freed |
|
inlinenoexceptinherited |
Reset all the control attributes of arc. That is: all control bits, the state and the counter are set to zero. The cookie is set to nullptr value
|
inlineinherited |
Reset all the arcs of graph (the control bits, the state, the counter and the cookie)
|
inlinenoexceptinherited |
Reset all the cookies to `nullptr for all the arcs of graph.
|
inlinenoexceptinherited |
Reset all the cookies to `nullptr for all the nodes of graph.
|
inlinenoexceptinherited |
Reset all the control attributes of node p. That is: all control bits, the state and the counter are set to zero. The cookie is set to nullptr value
|
inlineinherited |
Reset all the nodes of graph (the control bits, the state, the counter and the cookie)
|
inlinenoexceptinherited |
Linear search of an arc.
Search linearly an arc satisfying the condition op.
This method is some similar to exists_arc(); the difference is that it returns a pointer and its value indicates the success of search.
The complexity is  for the worst case.
for the worst case.
| [in] | op | the criteria. |
nullptr otherwise
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Linear search of an arc.
Search linearly an arc satisfying the condition op.
This method is some similar to exists_arc(); the difference is that it returns a pointer and its value indicates the success of search.
The complexity is 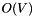 for the worst case.
for the worst case.
| [in] | p | pointer to the node from which the adjacent arcs want to be searched. |
| [in] | op | the criteria. |
nullptr otherwise
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Search an arc linking two nodes.
search_arc(src, tgt) searches an arc linking src with tgt. The method inspect the ars adjacent to src verifying whether a target is or not tgt.
This method is conceived for both directed and non directed graphs. But in the not directed case, the notion of source and target node has not much sense. The result of search_node(src, tgt) is the same than search_node(tgt, src).
search_directed()The complexity is $ 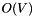 worst case.
worst case.
| [in] | src | source node [in] tgt target node |
nullptr otherwise.
|
inlinenoexceptinherited |
Search a directed arc linking two nodes.
search_directed_arc(src, tgt) searches an arc of form src --> tgt, on bot directed and non directed graphs.
| [in] | src | pinter to source node |
| [in] | tgt | pinter to target node |
nullptr otherwise.
|
inlinenoexceptinherited |
Search an incoming arc to a node satisfaying a condition.
search_in_arc(p, op) traveses the incoming arcs of p and search one for which op return true.
| [in] | p | pointer to the node. |
| [in] | op | operation to be executed on each arc in order to match certain search criteria. op must return true when the arc satisfies the search criteria. |
nullptr otherwise | anything | that op could throw |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Linear search of a node.
Search linearly a node satisfying the condition op.
This method is some similar to exists_node(); the difference is that it returns a pointer and its value indicates the success of search.
The complexity is 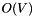 for the worst case.
for the worst case.
| [in] | op | the criteria. |
nullptr otherwise
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Search an outcoming arc to a node satisfaying a condition.
search_out_arc(p, op) traveses the outcoming arcs of p and search one for which op return true.
| [in] | p | pointer to the node. |
| [in] | op | operation to be executed on each arc in order to match certain search criteria. op must return true when the arc satisfies the search criteria. |
nullptr otherwise | anything | that op could throw |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlineinherited |
Temporal indication for preventing to other algorithms that an graph must be treated as a directed graph.
Sometimes (in Aleph-w ( 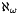 ) many times) is desirable to deal with a non-directed graph as if this was a directed one. Such is the case, for example, of functor
) many times) is desirable to deal with a non-directed graph as if this was a directed one. Such is the case, for example, of functor Random_Digraph, which is used for generating random digraphs. Of course, since Random_Digraph is designed for generating digraphs, it manages its internal state thinking that a digraph is generated.
Now, in a few circunstances, very often for practical purpuses (performace, easiness of coding, etc), a non-directed graph is wanted to be dealt as a directed one. In this case some algorithms need to know that the graph is in reality directed. In order to solve this ambiguity, the internal state that indicates that the graph is directed could be changed. In this way, foin order to instruct to Random_Digraph that deals a non-directed as a directed one, the flag "directed" is changed to true.
Of course, this technique is very very risky. Take into account that topological changing operations variate according to the directness of graph. Thus, to change the directed flag and then to insert and/or to remove nodes and/or arcs will mess everything and the chances of disater will be very high. For this reason, the use of this method is not recommended and its presence must be considered temporal while we find a more proper approach, concretely while Random_Digraph remains without to be refactored, which is, in fact, the unique part of Aleph-w ( 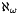 ) that temporally uses this method.
) that temporally uses this method.
|
inlinenoexcept |
Sort all the arcs of the graph according to a specific criteria.
The method takes an comparison operation between two arcs and sorts the arcs.
The comparison criteria should match the following signature:
bool cmp(Arc * a1, Arc * a2);
So, inside cmp you would access to the data arcs and would perform the comparison.
After execution of this method, provided that no new arcs are inserted or others sorts are not performed with a different criteria, it is guaranted that order of apparition of the arc by the Arc_Iterator will be sorted.
| [in,out] | cmp | operation of comparison that defines the sorting criteria |
|
inlinenoexcept |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexcept |
Sort all the nodes of the graph according to a specific criteria.
The method takes an comparison operation between two nodes and sorts the nodes.
The comparison criteria should match the following signature:
bool cmp(Node * a1, Node * a2);
So, inside cmp you would access to the data arcs and would perform the comparison.
After execution of this method, provided that no new nodes are inserted or others sorts are not performed with a different criteria, it is guaranted that order of apparition of the nodes by the Node_Iterator will be sorted.
| [in,out] | cmp | operation of comparison that defines the sorting criteria |
|
inlinenoexcept |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Conditioned traversal of all the arcs of a graph.
traverse_arc(operation) condionally traverses all the arcs of a graph and on each arc a executes operation(a). The operation must have the following functor structure:
bool operation(Arc * a)
This signature can be accomplished through a function pointer, a functor or a lambda (via the overloaded rvalue version). Note that there is a return value. If operation(p) returns true, then the next node is traversed. Otherwise the traversal stops and the remainder nodes are not visited.
if the graph type was GT then the arc type would be GT::Arc. In this primitive as well for the majority of functional primitives, you could declare the parameter types as auto and to leave to compiler to infer them. This could be more practical and easier for writing but it also could hide the true type and in some cases to do incomprehensible the the type.
The operation is  for the worst and average case.
for the worst and average case.
For example, supposse that we wish print out the arcs content for all the arcs. Then we could do it as follows:
g.traverse_arcs([] (auto a)
{
cout << a->get_info() << endl;
return true; // for instructing to visit the next node
});
operation, by example, to not return anything, not only they probably will not compile, but the diagnostic errors could be hard to undertand. Perhaps, on some compilers, bad signatures could compile. So, be sure to match the correct operation signature.| [in] | operation | operation to be performed on each arc. The operation must imperatively return a bool indicating whether or not the next arc must be visited. |
bool with the last operationresult. If true then all the arcs were visited and on each one operation executed. Otherwise, the traversal was stopped. | any | exception that could throw operation |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Conditioned traversal of all the adjacent arcs of a node.
traverse_arc(p, operation) condionally traverses all the arcs of the node p and on each arc a executes operation(a). The operation must have the following functor structure:
bool operation(Arc * a)
This signature can be accomplished through a function pointer, a functor or a lambda (via the overloaded rvalue version). Note that there is a bool return value. If operation(p) returns true, then the next node is traversed. Otherwise the traversal stops and the remainder nodes are not visited.
if the graph type was GT then the arc type would be GT::Arc. In this primitive as well for the majority of functional primitives, you could declare the parameter types as auto and to leave to compiler to infer them. This could be more practical and easier for writing but it also could hide the true type and in some cases to do incomprehensible the the type.
The operation is 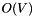 for the worst case, but it could be much less for sparsed graphs.
for the worst case, but it could be much less for sparsed graphs.
For example, supposse that we wish print out the arcs content for the nodes adjacent to the node p. Then we could do it as follows:
g.traverse_arcs(p, [] (auto a)
{
cout << a->get_info() << endl;
return true; // for instructing to visit the next node
});
operation, by example, to not return anything, not only they probably will not compile, but the diagnostic errors could be hard to undertand. Perhaps, on some compilers, bad signatures could compile. So, be sure to match the correct operation signature.| [in] | p | node from you want to access its adjacent arcs. |
| [in] | operation | operation to be performed on each arc. The operation must imperatively return a bool indicating whether or not the next arc must be visited. |
bool with the last operationresult. If true then all the arcs were visited and on each one operation executed. Otherwise, the traversal was stopped. | any | exception that could throw operation |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Traverse of arcs of a node according to specific arcs iterator.
traverse_arcs<Itor, Operation>(p, operation) is very similar a traverse_arcs(), except that this version receives the arc iterator as template parameter. Its use is intended to serve as implementation base for functional primitives on incoming and outcoming arcs.
| [in] | p | node to traverse its arcs |
| [in] | operation | to perform on each arc given by the iterator. The convention is the the same than for traverse methods. If operationreturn true, then the next arc is revised; otherwise the traversal stops. |
true if all the arcs were traversed; false otherwise. | whatever | could throw operation |
|
inlinenoexceptinherited |
Traverse the incoming arcs of node p executing the conditioned operation
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Conditioned traversal of all the nodes of a graph.
traverse_nodes(operation) condionally traverses all the nodes of a graph and on each node p executes operation(p). The operation must have the following functor structure:
bool operation(Node * p)
This signature can be accomplished through a function pointer, a functor or a lambda (via the overloaded rvalue version). Note that there is a return value. If operation(p) returns true, then the next node is traversed. Otherwise the traversal stops and the remainder nodes are not visited.
For example, supposse that we wish print out the nodes content for all the nodes. Then we could do it as follows:
g.traverse_nodes([] (auto p)
{
cout << p->get_info() << endl;
return true; // for instructing to visit the next node
});
traverse_nodes() is the heart of functional primitives on nodes of a graph. All other functional primitives depend on it. In general, ait is as fast as to directly iterate on the nodes.
The operation is 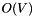 for the worst and average case.
for the worst and average case.
operation, by example, to not return anything, not only they probably will not compile, but the diagnostic errors could be hard to undertand. Perhaps, on some compilers, bad signatures could compile. So, be sure to match the correct operation signature.| [in] | operation | operation to be performed on each node. The operation must imperatively return a bool indicating whether or not the next node must be visited. |
bool with the last operationresult. If true then all the mode were visited and on each one operation executed. Otherwise, the traversal was stopped. | any | exception that could throw operation |
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
|
inlinenoexceptinherited |
Traverse the outcoming arcs of node p executing the conditioned operation
|
inlinenoexceptinherited |
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.