Collaboration diagram for Graphs:

Classes
class	Aleph::Bit_Fields

struct	Aleph::Graph_Attr

class	Aleph::Bellman_Ford< GT, Distance, Ait, NAit, SA >

struct	Aleph::Bellman_Ford_Negative_Cycle< GT, Distance, Ait, NAit, SA >

class	Aleph::Dijkstra_Min_Paths< GT, Distance, Itor, SA >
	Spanning tree calculation of all shortest paths from a given node according to Dijkstra's algorithm. More...

class	Aleph::Test_Eulerian< GT, SN, SA >

class	Aleph::Floyd_All_Shortest_Paths< GT, Distance, SA >

struct	Aleph::To_Graphviz< GT, Node_Attr, Arc_Attr, SN, SA >

struct	Aleph::Generate_Graphviz< GT, Write_Node, Write_Arc, Shade_Node, Shade_Arc, Dashed_Node, Dashed_Arc, SA, SN >

struct	GTNodeIterator< GT >

struct	GTArcIterator< GT >

struct	Cmp_Dlink_Node< GT, Cmp >

struct	Cmp_Dlink_Arc< GT, Cmp >

class	GTNodeCommon< NodeInfo >

class	GTArcCommon< ArcInfo >

class	GraphCommon< GT, Node, Arc >

class	GraphCommon< GT, Node, Arc >::Digraph_Iterator< Filter >

struct	GraphCommon< GT, Node, Arc >::Out_Filt

struct	GraphCommon< GT, Node, Arc >::In_Filt

class	Graph_Traverse< GT, Itor, Q, Show_Arc >

class	Aleph::Graph_To_Tree_Node< GT, Key, Convert, SA >

class	Aleph::Build_Grid< GT, Operation_On_Node, Operation_On_Arc >

class	Aleph::Test_Hamiltonian_Sufficiency< GT, SN, SA >

class	Aleph::IO_Graph< GT, Load_Node, Store_Node, Load_Arc, Store_Arc, NF, AF >

class	Aleph::Kruskal_Min_Spanning_Tree< GT, Distance, SA >

class	Aleph::Prim_Min_Spanning_Tree< GT, Distance, SA >

class	Aleph::Random_Graph< GT, Init_Node, Init_Arc >

class	Aleph::Test_Single_Graph< GT, SN, SA >

class	Aleph::Tarjan_Connected_Components< GT, Itor, SA >

class	Aleph::Compute_Cycle_In_Digraph< GT, Itor, SA >

class	Aleph::Topological_Sort< GT, Itor, SA >

class	Aleph::Q_Topological_Sort< GT, Itor, SA >

class	Aleph::Graph_Anode< Node_Info >

class	Aleph::Array_Digraph< __Graph_Node, __Graph_Arc >

class	Aleph::Compute_Bipartite< GT, SA >

class	Aleph::Compute_Maximum_Cardinality_Bipartite_Matching< GT, Max_Flow, SA >

class	Aleph::Build_Subgraph< GT, SA >

class	Aleph::Inconnected_Components< GT, SA >

class	Aleph::Compute_Cut_Nodes< GT, SA >

class	Aleph::Dyn_Graph< GT >

class	Aleph::Find_Path_Depth_First< GT, Itor, SA >

class	Aleph::Find_Path_Breadth_First< GT, Itor, SA >

class	Aleph::Directed_Find_Path< GT, Itor, SA >

struct	Aleph::Graph_Node< __Node_Info >

struct	Aleph::Graph_Arc< __Arc_Info >

struct	Aleph::List_Graph< __Graph_Node, __Graph_Arc >::Node_Iterator

class	Aleph::List_Graph< __Graph_Node, __Graph_Arc >::Node_Arc_Iterator

class	Aleph::List_Graph< __Graph_Node, __Graph_Arc >

struct	Aleph::Dft_Show_Arc< GT >

struct	Aleph::Node_Arc_Iterator< GT, Show_Arc >

struct	Aleph::Arc_Iterator< GT, Show_Arc >

struct	Aleph::Dft_Show_Node< GT >

class	Aleph::Node_Iterator< GT, Show_Node >

class	Aleph::__Out_Filt< GT >

class	Aleph::__In_Filt< GT >

class	Aleph::Digraph_Iterator< GT, Filter >

struct	Aleph::Out_Iterator< GT, Show_Arc >

class	Aleph::In_Iterator< GT, SA >

class	Aleph::Operate_On_Nodes< GT, Operation, SN >

class	Aleph::Operate_On_Arcs< GT, Operation, SA >

class	Aleph::Path< GT >::Iterator

class	Aleph::Path< GT >

struct	Aleph::Dft_Copy_Node< GTT, GTS >

struct	Aleph::Dft_Copy_Arc< GTT, GTS >

class	Aleph::Copy_Graph< GT, SN, SA >

struct	Aleph::Painted_Min_Spanning_Tree< GT, Distance >

class	Aleph::Nodes_Index< GT, Compare, Tree, SN >

class	Aleph::Arcs_Index< GT, Compare, Tree, SA >

struct	Aleph::Default_Visit_Op< GT >

class	Aleph::Depth_First_Traversal< GT, Operation, SA >

class	Aleph::Breadth_First_Traversal< GT, Operation, SA >

struct	Aleph::Distance_Compare< GT, Distance >

class	Aleph::Invert_Digraph< GT, SA >

class	Aleph::Dft_Dist< GT >

class	Aleph::Total_Cost< GT, Distance, SA >

class	Aleph::IndexArc< GT, Tree, SA >

class	Aleph::Index_Graph< GT, Compare, Tree >

class	Aleph::IndexNode< GT, Compare, Tree, SN >

class	Aleph::Edge_Connectivity< GT, Max_Flow >

class	Aleph::Compute_Min_Cut< GT, Max_Flow, SA >

class	Aleph::Map_Matrix_Graph< GT, SA >

class	Aleph::Matrix_Graph< GT, SA >

class	Aleph::Ady_Mat< GT, __Entry_Type, SA >

class	Aleph::Bit_Mat_Graph< GT, SA >

class	Aleph::Net_Sup_Dem_Node< Node_Info, F_Type >

class	Aleph::Net_Sup_Dem_Graph< NodeT, ArcT >

class	Aleph::Net_Cap_Node< Node_Info, F_Type >

struct	Aleph::Net_Cost_Arc< Arc_Info, F_Type >

struct	Aleph::Graph_Snode< Node_Info >

class	Aleph::Graph_Sarc< Arc_Info >

class	Aleph::List_SGraph< __Graph_Node, __Graph_Arc >::Node_Iterator

class	Aleph::List_SGraph< __Graph_Node, __Graph_Arc >::Node_Arc_Iterator

class	Aleph::List_SGraph< __Graph_Node, __Graph_Arc >

class	Aleph::List_SDigraph< __Graph_Node, __Graph_Arc >

class	Aleph::Find_Depth_First_Spanning_Tree< GT, SA >

class	Aleph::Find_Breadth_First_Spanning_Tree< GT, SA >

class	Aleph::Build_Spanning_Tree< GT >

class	Aleph::Is_Graph_Acyclique< GT, SA >

class	Aleph::Has_Cycle< GT, SA >

class	Test_Connectivity< GT, SA >

class	Aleph::Test_For_Cycle< GT, SA >

class	Aleph::Test_For_Path< GT, SA >

class	Aleph::Warshall_Compute_Transitive_Clausure< GT, SA >

Macros
#define	NODE_BITS(p) ((p)->attrs.control_bits)

#define	NODE_COUNTER(p) ((p)->attrs.counter)

#define	NODE_COLOR(p) ((p)->attrs.counter)

#define	IS_NODE_VISITED(p, bit) (NODE_BITS(p).get_bit(bit))

#define	NODE_COOKIE(p) ((p)->attrs.cookie)

#define	ARC_COUNTER(p) ((p)->attrs.counter)

#define	ARC_COLOR(p) ((p)->attrs.counter)

#define	ARC_BITS(p) ((p)->attrs.control_bits)

#define	IS_ARC_VISITED(p, bit) (ARC_BITS(p).get_bit(bit))

#define	ARC_COOKIE(p) ((p)->attrs.cookie)

Typedefs
template<class GT >
using	Aleph::ArcPair = tuple< typename GT::Arc , typename GT::Node >

template<class GT >
using	Aleph::__Out_Iterator = typename GT::Out_Iterator

template<class GT >
using	Aleph::__In_Iterator = typename GT::In_Iterator

Enumerations
enum	Aleph::Graph_Bits { Depth_First, Breadth_First, Test_Cycle, Find_Path, Euler, Maximum_Flow, Spanning_Tree, Build_Subtree, Convert_Tree, Cut, Min, Num_Bits_Graph }

Functions
template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >
void	Aleph::generate_graphpic (const GT &g, const double &xdist, const double &, std::ostream &output)

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class Dashed_Node , class Dashed_Arc , class SA , class SN >
void	Aleph::generate_graphviz (const GT &g, std::ostream &output, const string &rankdir="TB", float ranksep=0.2, float nodesep=0.2)

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >
void	Aleph::generate_graphviz (const GT &g, std::ostream &out, Node_Attr node_attr=Node_Attr(), Arc_Attr arc_attr=Arc_Attr(), const string &rankdir="TB")

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >
void	Aleph::digraph_graphviz (const GT &g, std::ostream &out, Node_Attr node_attr=Node_Attr(), Arc_Attr arc_attr=Arc_Attr(), const string &rankdir="LR")

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >
size_t	Aleph::rank_graphviz (const GT &g, std::ostream &out, Node_Attr node_attr=Node_Attr(), Arc_Attr arc_attr=Arc_Attr(), const string &rankdir="LR")

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >
void	Aleph::generate_cross_graph (GT &g, const size_t &nodes_by_level, const double &xdist, const double &ydist, std::ostream &out)

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >
void	Aleph::generate_net_graph (GT &g, const size_t &nodes_by_level, const double &xdist, const double &ydist, std::ostream &out)

template<class GT , typename Key , class Convert , class SA = Dft_Show_Arc<GT>>
Tree_Node< Key > *	Aleph::graph_to_tree_node (GT &g, typename GT::Node *groot)

template<class GT >
void	Aleph::kosaraju_connected_components (const GT &g, DynList< GT > &blk_list, DynList< typename GT::Arc *> &arc_list)

template<class GT >
DynList< DynList< typename GT::Node * > >	Aleph::kosaraju_connected_components (const GT &g)

template<class Mat >
void	find_min_path (Mat &p, typename Mat::Node src_node, typename Mat::Node tgt_node, Path< typename Mat::Graph_Type > &path)

template<class Mat >
void	find_min_path (Mat &p, const long &src_index, const long &tgt_index, Path< typename Mat::Graph_Type > &path)

GT	Aleph::Random_Graph_Base< GT, Init_Node, Init_Arc >::sufficient_hamiltonian (const size_t &__num_nodes, const double &p=0.5)

GT	Aleph::Random_Graph< GT, Init_Node, Init_Arc >::sufficient_hamiltonian (const size_t &__num_nodes, const double &p=0.5)

template<class GT , class SA = Dft_Show_Arc<GT>>
void	Aleph::compute_bipartite (const GT &g, DynDlist< typename GT::Node > &l, DynDlist< typename GT::Node > &r)

template<class GT , template< class > class Max_Flow = Ford_Fulkerson_Maximum_Flow, class SA = Dft_Show_Arc<GT>>
void	Aleph::compute_maximum_cardinality_bipartite_matching (const GT &g, DynDlist< typename GT::Arc *> &matching)

template<class GT , class SN = Dft_Show_Node<GT>>
void	Aleph::for_each_node (const GT &g, std::function< void(typename GT::Node *)> operation, SN sn=SN()) noexcept(noexcept(operation) and noexcept(sn))

template<class GT , class SA = Dft_Show_Arc<GT>>
void	Aleph::for_each_arc (const GT &g, std::function< void(typename GT::Arc *)> operation, SA sa=SA()) noexcept(noexcept(operation) and noexcept(sa))

template<class GT , class SA = Dft_Show_Arc<GT>>
void	Aleph::for_each_arc (const GT &, typename GT::Node p, std::function< void(typename GT::Arc )> operation, SA sa=SA()) noexcept(noexcept(operation) and noexcept(sa))

template<class GT , class SN = Dft_Show_Node<GT>>
bool	Aleph::forall_node (const GT &g, std::function< bool(typename GT::Node *)> cond, SN sn=SN()) noexcept(noexcept(cond) and noexcept(sn))

template<class GT , class SA = Dft_Show_Arc<GT>>
bool	Aleph::forall_arc (const GT &g, std::function< bool(typename GT::Arc *)> cond, SA sa=SA()) noexcept(noexcept(cond) and noexcept(sa))

template<class GT , class SA = Dft_Show_Arc<GT>>
bool	Aleph::forall_arc (typename GT::Node p, std::function< bool(typename GT::Arc )> cond, SA sa=SA()) noexcept(noexcept(cond) and noexcept(sa))

template<class GT , typename T , template< typename > class Container = DynList, class SN = Dft_Show_Node<GT>>
Container< T >	Aleph::nodes_map (GT &g, std::function< T(typename GT::Node *)> transformation, SN sn=SN())

template<class GT , typename T , template< typename > class Container = DynList, class SA = Dft_Show_Arc<GT>>
Container< T >	Aleph::arcs_map (GT &g, std::function< T(typename GT::Arc *)> transformation, SA sa=SA())

template<class GT , typename T , template< typename > class Container = DynList, class SA = Dft_Show_Arc<GT>>
Container< T >	Aleph::arcs_map (GT &g, typename GT::Node p, std::function< T(typename GT::Arc )> transformation, SA sa=SA())

template<class GT , typename T , class SN = Dft_Show_Node<GT>>
T	Aleph::foldl_nodes (GT &g, const T &init, std::function< T(const T &, typename GT::Node *)> operation, SN sn=SN()) noexcept(noexcept(operation) and noexcept(sn) and std::is_nothrow_copy_assignable< T >::value)

template<class GT , typename T , class SA = Dft_Show_Arc<GT>>
T	Aleph::foldl_arcs (GT &g, const T &init, std::function< T(const T &, typename GT::Arc *)> operation, SA sa=SA()) noexcept(noexcept(operation) and noexcept(sa) and std::is_nothrow_copy_assignable< T >::value)

template<class GT , typename T , class SA = Dft_Show_Arc<GT>>
T	Aleph::foldl_arcs (GT &g, typename GT::Node p, const T &init, std::function< T(const T &, typename GT::Arc )> operation, SA sa=SA()) noexcept(noexcept(operation) and noexcept(sa) and std::is_nothrow_copy_assignable< T >::value)

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< typename GT::Node * >	Aleph::out_nodes (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< typename GT::Node * >	Aleph::in_nodes (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< typename GT::Arc * >	Aleph::out_arcs (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< typename GT::Arc * >	Aleph::in_arcs (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< typename GT::Arc * >	Aleph::arcs (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< ArcPair< GT > >	Aleph::in_pairs (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
DynList< ArcPair< GT > >	Aleph::out_pairs (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
size_t	Aleph::in_degree (typename GT::Node *p, SA sa=SA())

template<class GT , class SA = Dft_Show_Arc<GT>>
size_t	Aleph::out_degree (typename GT::Node *p, SA sa=SA())

template<class GT , class Itor , class Operation >
bool	Aleph::traverse_arcs (typename GT::Node *p, Operation op=Operation()) noexcept(noexcept(op))

template<class GT , class Itor , class Operation >
void	Aleph::for_each_arc (typename GT::Node *p, Operation op=Operation()) noexcept(noexcept(op))

template<class GT , class Op >
bool	Aleph::traverse_in_arcs (typename GT::Node *p, Op op=Op()) noexcept(noexcept(op))

template<class GT , class Op >
void	Aleph::for_each_in_arc (typename GT::Node *p, Op op=Op()) noexcept(noexcept(op))

template<class GT , class Op >
bool	Aleph::traverse_out_arcs (typename GT::Node *p, Op op=Op()) noexcept(noexcept(op))

template<class GT , class Op >
void	Aleph::for_each_out_arc (typename GT::Node *p, Op op=Op()) noexcept(noexcept(op))

template<class GT , class SA = Dft_Show_Arc<GT>>
GT::Arc *	Aleph::search_arc (const GT &g, typename GT::Node src, typename GT::Node tgt, SA sa=SA()) noexcept

template<class GT , class SA = Dft_Show_Arc<GT>>
GT::Arc *	Aleph::search_directed_arc (const GT &, typename GT::Node src, typename GT::Node tgt, SA sa=SA()) noexcept

template<class GT >
GT::Node *	Aleph::mapped_node (typename GT::Node *p) noexcept

template<class GT >
void	Aleph::copy_graph (GT &gtgt, const GT &gsrc, const bool cookie_map=false)

template<class GT >
void	Aleph::clear_graph (GT &g) noexcept

template<class GT >
Path< GT >	Aleph::find_path_depth_first (const GT &g, typename GT::Node start_node, typename GT::Node end_node)

template<class GTS , class GTT >
void	Aleph::map_nodes (typename GTS::Node p, typename GTT::Node q) noexcept

template<class GTS , class GTT >
void	Aleph::map_arcs (typename GTS::Arc p, typename GTT::Arc q) noexcept

template<class GTT , class GTS , class Copy_Node = Dft_Copy_Node<GTT, GTS>, class Copy_Arc = Dft_Copy_Arc<GTT, GTS>>
void	Aleph::inter_copy_graph (GTT &gtgt, const GTS &gsrc, const bool cookie_map=false)

template<class GT >
size_t	Aleph::depth_first_traversal (const GT &g, typename GT::Node start_node, bool(visit)(const GT &g, typename GT::Node , typename GT::Arc ))

template<class GT >
size_t	Aleph::breadth_first_traversal (const GT &g, typename GT::Node start, bool(visit)(const GT &, typename GT::Node , typename GT::Arc ))

template<class GT >
Path< GT >	Aleph::find_path_breadth_first (const GT &g, typename GT::Node start, typename GT::Node end)

template<class GT >
bool	Aleph::test_connectivity (const GT &g)

template<class GT >
bool	Aleph::test_for_cycle (const GT &g, typename GT::Node *src)

template<class GT >
bool	Aleph::test_for_path (const GT &g, typename GT::Node start_node, typename GT::Node end_node)

template<class GT >
DynList< GT >	Aleph::inconnected_components (const GT &g)

template<class GT >
void	Aleph::build_subgraph (const GT &g, GT &sg, typename GT::Node *g_src, size_t &node_count)

template<class GT >
GT	Aleph::find_depth_first_spanning_tree (const GT &g, typename GT::Node *gnode)

template<class GT >
GT	Aleph::find_breadth_first_spanning_tree (GT &g, typename GT::Node *gp)

template<class GT >
GT	Aleph::build_spanning_tree (const DynArray< typename GT::Arc *> &arcs)

template<class GT >
DynList< typename GT::Node * >	Aleph::compute_cut_nodes (const GT &g, typename GT::Node *start)

template<class GT >
long	Aleph::paint_subgraphs (const GT &g, const DynList< typename GT::Node *> &cut_node_list)

template<class GT >
GT	Aleph::map_subgraph (const GT &g, const long color)

template<class GT >
std::tuple< GT, DynList< typename GT::Arc * > >	Aleph::map_cut_graph (const GT &g, const DynList< typename GT::Node *> &cut_node_list)

template<class GT >
GT	Aleph::invert_digraph (const GT &g)

template<class GT , template< class > class Max_Flow = Random_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>
long	Aleph::edge_connectivity (GT &g)

template<class GT , template< class > class Max_Flow = Heap_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>
long	Aleph::compute_min_cut (GT &g, Aleph::set< typename GT::Node > &l, Aleph::set< typename GT::Node > &r, DynDlist< typename GT::Arc *> &cut)

template<class GT , template< class > class Max_Flow = Random_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>
long	Aleph::vertex_connectivity (GT &g)

template<class GT , class SA = Dft_Show_Arc<GT>>
void	Aleph::warshall_compute_transitive_clausure (GT &g, Bit_Mat_Graph< GT, SA > &mat)

template<class Mat >
void	Aleph::find_min_path (Mat &p, const long &src_index, const long &tgt_index, Path< typename Mat::Graph_Type > &path)

Variables
const unsigned char	Aleph::Processed

const unsigned char	Aleph::Processing

const unsigned char	Aleph::Unprocessed

Detailed Description

Introduction

Many combinatorial problems can be modeled and solved through Aleph-w ( $\aleph_\omega$ ) graphs.

There are three types of graphs in Aleph-w ( $\aleph_\omega$ ):

List_Digraph<Node, Arc>: graph represented with doubly linked lists.
List_SGraph<Node, Arc>: graph represented with single linked lists.
Array_Graph<Node, Arc>: graph represented with dynamic arrays.

All the three classes export the same interface. What differentiates them is their performance qualities in speed and space comsuption.

Historically, the first Aleph-w ( $\aleph_\omega$ ) graph class was List_Graph. This class is very versatile and dynamic in the sense that it allow very fast topological modifications on the graph. By "topological modification" we intend to say that nodes and/or arc are inserted and/or removed. The dynamic sense consists on the possibility that these operations are done very frequently in $O(1)$ . 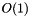List_Graph in since the choice of fact for applications requering to build partial and/or many graph are very often. However, this speed pays its price in space consumption.

List_SGraph was designed in order to reduce the space consumption of List_Graph. This is managed by using single lists instead of double ones, what reduces aproximatively 4 pointers by node and arc. However, the remove_node() method is slower $O(E)$ , since it requires to traverse all the arcs ir order to remove the arcs pointed to the removed node. So, this class could be very time expensive for application that dinamically remove nodes. Although this class is fully functional and (we hope) correct, we are considering remove it or simply not support it longer in next library releases.

Finally, the class Array_Graph models graphs whose internal representation uses dinamic arrays in order to save the adjacency lists. According our experience, we find this class as a very good trade off between performance and space consumption. The remove_node() operation is still $O(E)$ , but the remaining topological operations are 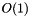$O(1)$ and definitively this class occupies much less space than the list versions. We recommend to use this class unless that you require to remove nodes many times. There are a few of applications where you perform calculation by removing nodes from a graph. For this type of case, consider to use another graph.

Specifiying a graph

In order to specify a graph and to do computations on it, the first thing that you must do is to define the types of data to store in the nodes and the arcs. Often the nodes and arcs are associated with many data. By example, a graph of cities could map the cities with the nodes and the distances and other sort of costs with the arcs. For each city (node) one could associate coordinates, the name, its population, etc. Now, in order to save space, it is very important that you only associate to the node the required data needed for the graph computations. Remember, the more fat is the data to associate to a node or arc, the more space the graph will use. So, use ids to the data, not all the data. In those case where the data resides in memory associate pointers to it. Of course, this remarks apply specially to the large scale graphs. If your graph is small, then perhaps you must not worry too much.

Once you already have defined data types that you will store in the nodes and arcs, then you must declare the node and arc that you will use.

The graphs interface requires the following specificaction convention:

Node definition: in this phase you define the type of data to store in the nodes and then you declare the node.
Arc definition: in the same way than for nodes, you define the type of data to store in the arcs. Then you declare the arc
Graph definition: once defined the nodes and arcs structure, you declare the graph by passing it the nodes and arcs types previously defined.

It is strongly recommended to do these phased by using aliases, typedef or using, to the node, arc and graph types.

Specifiying the node

Before to declare a Aleph-w ( 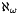$\aleph_\omega$ ) graph, you must imperatively you must have declared the node. The node types are:

Graph_Node<T>: for List_Graph
Graph_Snode<T>: for List_SGraph
Graph_Anode<T>: for Array_Graph

If you want to use Point as type of nodes, then you could declare:

using My_Node = Graph_Node<Point>;

Here you have expressed that the nodes of your graph contain data of type Point and that you will use List_Graph as graph type (the Aleph-w ( 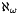$\aleph_\omega$ ) graph whose representation is with doubly linked lists.

Specifiying the arc

For the arcs you must also declare its type. There are three types of arcs according to the graph type:

Graph_Arc<T>: for List_Graph
Graph_Sarc<T>: for List_SGraph
Graph_Aarc<T>: for Array_Graph

By example, following the previous example, if the weights are euclidian distances between the points, ten you could declare an arc as follows:

using My_Arc = Grap_Arc<double>;

Specifying the Graph

Once you have defined the node and the arc of your graph, you are ready for declare the graph. For the previous example, that would be as follows:

using Euclidian_Graph = Graph_List<My_Node. My_Arc>;

Now, you can instantiate graphs by using the alias Euclidian_Graph, some as:

Euclidian_Graph g;

Although you have already defined your node and arc with aliases, the interface exports two internal aliases that could be considered as subclasses:

Euclidian_Graph::Node, and
Euclidian_Graph::Arc

You will need to know the types of nodes and arc in order to perform many operations on the graph. In our experience, it is more readable to use the these aliases instead of those that you declared when you was specifiying the graph. The following code snippet traverses all the arcs of a Euclidian_Graph graph:

Euclidian_Graph g
some operations; by example insert nodes and arcs ...
for (auto it = g.get_arc_it(); it.has_curr(); it.next())
  {
    Euclidian_Graph::Arc * arc = it.get_curr(); 
    do something with the arc
  }

Filtered iterators

The graph classes export several iterators: Node_Iterator, Arc_Iterator, Node_Arc_Iterator, Out_Iterator and In_Iterator. These iterator are exported as subclasses of the graph class. Suppose, for example, that you are using a class Map based on Array_Graph class (but it could have perfectly been base on any other graph class) and the graph is named g. Then, you could iterate on all the arcs through some such as:

for (auto it = g.get_arc_it(); it.has_cur(); it.next())
  auto arc = it.get_curr(); // each arc of the graph is seen

Now, there are several, perhaps many, situations where not all the arcs must be proceses, but a subset of them satisfaying a particular condition. In these cases, the filtered iteratos come for us.

As seen in the class Filter_Iterator, a filtered iterator is almost exactly the same thing than a normal iterator. The subtle difference is that on it operates a filter condition that filters all the items satisfaying a special condition. Let's show a brief but constructive example.

Un brief example

Suppose that your graph represents pathways of automotive transportation. Node are the cities and arcs are the pathways. Now suppose that your pathways are classified in Highway, Road and Trail. Now suppose that you wish to solve a problem that only envolves highways; for example, you want to find the shortest path between two cities connected by only highways. Then you could specify an filter that catches highways:

struct Only_Highway
{
  bool operator () (GT::Arc * a) 
  {
    return a->get_info().type == Highway;
  }
};

Now, if your shortest path algorithm receives this filter, this will only see highways and its results will only contain highways.

Convention about filtered iterators

For each subclass iterator on a graph, it is exported a filtered iterator with the same name of subclassed one. Thus, for the subclass GT::Arc_Iterator exists a filtered version named Arc_Iterator and so on for the remainder iterator subclasses on the graphs.

The filtered iterators have a great importance in Aleph-w ( 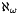$\aleph_\omega$ ) algorithms on graphs, since almost every algorithm operates with filtered iterator.

When to use then?

The short answer is: almost always!

Filtered iterators have of course a light but constant impact on performance. For each seen graph object a boolean predicate is tested. So, if you know that your algorithm does not require to filter, the use the subclass iterator. But if, in pursuit of generalization your algorithm could profit the filtered version, then design your algorithm on filtered iterator. In this way you will provide generality, which allows to reuse algorithms in a transparent way.

A very good and concrete example of intensive use of filtered iterator is for solving the problem of maximizing a network flow at minimum cost. First, in order to manage the residual net, the arcs are filtered according to source node. Second, the residual cut arcs are also filtered according to flow value; if the flow is equal to the capacity then the arc is filtered. Third, in order to detect negative cycles the Bellman-Ford algorithm is used with a filter that only sees the arcs cost.

Macro Definition Documentation

◆ ARC_BITS

#define ARC_BITS ( p ) ((p)->attrs.control_bits)

Return the control bits of arc p

◆ ARC_COLOR

#define ARC_COLOR ( p ) ((p)->attrs.counter)

Return the color of arc p

◆ ARC_COOKIE

#define ARC_COOKIE ( p ) ((p)->attrs.cookie)

Return the arc cookie

◆ ARC_COUNTER

#define ARC_COUNTER ( p ) ((p)->attrs.counter)

Return the counter of arc p

◆ IS_ARC_VISITED

#define IS_ARC_VISITED	(	p,
		bit
	)	(ARC_BITS(p).get_bit(bit))

Determine whether the bit field is or not set to one

Parameters

p	pointer to arc
bit	number of bit to be read

Returns: true if bit is 1; false otherwise (bit is set to 0)

◆ IS_NODE_VISITED

#define IS_NODE_VISITED	(	p,
		bit
	)	(NODE_BITS(p).get_bit(bit))

Determine whether the control bit is set or not to one

Parameters

p	pointer to the node
bit	number of bit to read

Returns: true if the bit is 1; false if 0

◆ NODE_BITS

#define NODE_BITS ( p ) ((p)->attrs.control_bits)

Get the control bits of a node.

◆ NODE_COLOR

#define NODE_COLOR ( p ) ((p)->attrs.counter)

Synonymous of NODE_COUNTER

◆ NODE_COOKIE

#define NODE_COOKIE ( p ) ((p)->attrs.cookie)

Return the node cookie

◆ NODE_COUNTER

#define NODE_COUNTER ( p ) ((p)->attrs.counter)

Get the counter of a node.

Typedef Documentation

◆ __In_Iterator

template<class GT >

using Aleph::__In_Iterator = typedef typename GT::In_Iterator

Basic iterator for outcoming arcs of a node.

◆ __Out_Iterator

template<class GT >

using Aleph::__Out_Iterator = typedef typename GT::Out_Iterator

Basic iterator for outcoming arcs of a node.

◆ ArcPair

template<class GT >

using Aleph::ArcPair = typedef tuple<typename GT::Arc*, typename GT::Node*>

Alias used for encapsulating a pair of arc and node (related between them).

Enumeration Type Documentation

◆ Graph_Bits

enum Aleph::Graph_Bits

Bit numbers of nodes or arcs.

Nodes y arcs of graph have as control attributes (internal representation of state), a set of bits. These are their numbers named according to their use by the library.

You can use then for purposes other than the suggested name. However, be careful.

See also: Bit_Fields

Function Documentation

◆ arcs()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<typename GT::Arc*> Aleph::arcs	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return all the filtered arcs related to p

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Here is the call graph for this function:

Here is the caller graph for this function:

◆ arcs_map() [1/2]

template<class GT , typename T , template< typename > class Container = DynList, class SA = Dft_Show_Arc<GT>>

Container<T> Aleph::arcs_map	(	GT &	g,
		std::function< T(typename GT::Arc *)>	transformation,
		SA	sa = `SA()`
	)

Map the filtered arcs of a graph to a transformed type.

Parameters

[in]	g	the grapg
[in]	transformation	function `Arc*` –> T`
[in]	sa	arc filter

Returns: a Container<T> object with all the arcs mapped through the transformation

Here is the caller graph for this function:

◆ arcs_map() [2/2]

template<class GT , typename T , template< typename > class Container = DynList, class SA = Dft_Show_Arc<GT>>

Container<T> Aleph::arcs_map	(	GT &	g,
		typename GT::Node *	p,
		std::function< T(typename GT::Arc *)>	transformation,
		SA	sa = `SA()`
	)

Map the filtered nodes of node graph to a transformed type.

Parameters

[in]	g	the graph
[in]	p	node pointer
[in]	transformation	function `Node*` –> T`
[in]	sn	node filter

Returns: a Container<T> object with all the nodes arcs mapped through the transformation

◆ breadth_first_traversal()

template<class GT >

size_t Aleph::breadth_first_traversal	(	const GT &	g,
		typename GT::Node *	start,
		bool()(const GT &, typename GT::Node , typename GT::Arc *)	visit
	)

inline

Generic breadth first traversal of a graph.

This traverses the graph g form start_node in breadth first order. On each node, a visit function is called, whose signature must match as follows:

bool visit(const GT & g, GT::Node * curr, GT::Arc * from)

g is the graph, curr is the currently visited node and from is the arc from whom curr was discovered. If visit returns false then the traversal continues; otherwise it stops.

The traversal uses the contro Breadth_First

Parameters

[in]	g	the graph
[in]	start_node	the starting node
[in]	visit	function

Returns: the number of visited nodes

See also: depth_first_traversal() test_connectivity()

◆ build_spanning_tree()

template<class GT >

GT Aleph::build_spanning_tree ( const DynArray< typename GT::Arc *> & arcs )

Build a spanning tree tree whose arcs are stored in a dynamic array.

This function construct a spanning tree into a graph object given the arcs that comprises the tree.

Although this function is conceived for managing trees, it could eventually be used for graphs; for instance, the graph could contain cycles and this could happen even if the number of arcs is lesser than the number of nodes. Of course, it is not intended to use an array for storing a full graph.

Parameters

[in] arcs dynamic array containing the arcs part of tree.

Returns: a graph containg the tree defined by arcs array

Exceptions

bad_alloc if there is no enough memory

Here is the call graph for this function:

Here is the caller graph for this function:

◆ build_subgraph()

template<class GT >

void Aleph::Aleph::build_subgraph	(	const GT &	g,
		GT &	sg,
		typename GT::Node *	g_src,
		size_t &	node_count
	)

inline

Build a mapped subgraph of g from a starting node.

build_subgraph(g, sg, g_src, node_count) traverses in depth first order the graph g from a starting node g_src and builds in sg a mapped copy of all nodes and arcs reachable from g_src. So, it will discover all what is connected to g_src.

node_count accumulates the number of visited nodes.

The function uses the control bint Build_Subtree.

This function is more used as helper for inconnected_components().

Parameters

[in]	g	the original graph
[out]	sg	an initially empty graph where the mappeing will be put
[in]	g_src	pointer to initial node where start the mapping
[in,out]	node_count	counter of visited nodes

Exceptions

bad_alloc if there is no enough memory

See also: inconnected_components() copy_graph()

◆ clear_graph()

template<class GT >

void Aleph::clear_graph ( GT & g )

inlinenoexcept

Clean a graph: all its nodes and arcs are removed and freed.

Parameters

[in] g the graph

Here is the caller graph for this function:

◆ compute_bipartite()

template<class GT , class SA = Dft_Show_Arc<GT>>

void Aleph::compute_bipartite	(	const GT &	g,
		DynDlist< typename GT::Node *> &	l,
		DynDlist< typename GT::Node *> &	r
	)

Toma un grafo bipartido y calcula los conjuntos de particiÃ³n.

Un grafo es bipartido si puede dividirse en dos subconjuntos l y r tal que todo nodo de l sÃ³lo tiene arcos hacia nodos de r y viceversa.

compute_bipartite(g,l,r) toma un grafo bipartido g y calcula los conjuntos de biparticiÃ³n nombrados por los parÃ¡metros l y r, respectivamente.

Parameters

[in]	g	el grafo bipartido.
[out]	l	un conjunto particiÃ³n.
[out]	r	un conjunto particiÃ³n.

Exceptions

domain_error	si durante el cÃ¡lculo se determina que el grafo no es bipartido.
bad_alloc	si no hay suficiente memoria.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ compute_cut_nodes()

template<class GT >

DynList<typename GT::Node*> Aleph::compute_cut_nodes	(	const GT &	g,
		typename GT::Node *	start
	)

Compute the articulation (or cut) points of a graph.

The control bits Depth_First and Cut are used.

This function could combine it with paint_subgraphs() in order to paint the different components separated by the cut points.

Mapped copies of components could be computed with map_subgraph() and map_cut_graph() on a grap peviously painted.

g must be connected.

Parameters

[in]	g	the graph
[in]	start	a starting node by where to star the calculations

Returns: A list of node corresponding to thge cut coints

Exceptions

bad_alloc if there is no enough memory

See also: paint_subgraphs() map_subgraph() map_cut_graph()

◆ compute_maximum_cardinality_bipartite_matching()

template<class GT , template< class > class Max_Flow = Ford_Fulkerson_Maximum_Flow, class SA = Dft_Show_Arc<GT>>

void Aleph::compute_maximum_cardinality_bipartite_matching	(	const GT &	g,
		DynDlist< typename GT::Arc *> &	matching
	)

Calcula el emparejamiento de cardinalidad mÃ¡xima de un grafo bipartido.

compute_maximum_cardinality_bipartite_matching(g,matching) recibe un grafo bipartido g y calcula el mÃ¡ximo emparejamiento bipartido en la lista matching.

El procedimiento calcula los conjuntos de biparticiÃ³n, luego construye una red capacitada unitaria equivalente y sobre ella invoca a un algoritmo de maximizaciÃ³n de flujo.

La rutina maneja dos parÃ¡metros tipo:

GT el tipo de grafo bipartido
Max_Flow el algoritmo de maximizaciÃ³n de flujo a emplear para realizar el cÃ¡lculo

Parameters

[in]	g	el grafo bipartido.
[out]	matching	lista de arcos componentes del emparejamiento.

Exceptions

bad_alloc si no hay suficiente memoria.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ compute_min_cut()

template<class GT , template< class > class Max_Flow = Heap_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>

long Aleph::compute_min_cut	(	GT &	g,
		Aleph::set< typename GT::Node *> &	l,
		Aleph::set< typename GT::Node *> &	r,
		DynDlist< typename GT::Arc *> &	cut
	)

Calcula el corte mÃnimo de un grafo.

compute_min_cut(g, l, r, cut) indaga la conectividad en arcos del grafo g y retorna los conjuntos de nodos y arcos que conforman el corte.

El algoritmo construye una red capacitada unitaria equivalente y mediante sucesivas maximizaciones de flujo indaga la conectividad en arcos.

La rutina recibe dos parÃ¡etros tipo:

GT: el tipo grafo sobre al cual se le desea averiguar su conectividad.
Max_Flow el algoritmo de maximizaciÃ³n de flujo a emplear para averiguar conectividad.

Parameters

[in]	g	el grafo sobre el cual se desea calcular el corte mÃnimo.
[out]	l	un conjunto de nodos origen que involucra los arcos parte del corte.
[out]	r	un conjunto de nodos destino que involucra los arcos parte del corte y que son destino de los nodos en l.
[out]	cut	el conjunto de arcos parte del corte.

Returns: la conectividad en arcos del grafo.

Exceptions

bad_alloc si no hay suficiente memoria.

Here is the call graph for this function:

◆ copy_graph()

template<class GT >

void Aleph::copy_graph	(	GT &	gtgt,
		const GT &	gsrc,
		const bool	cookie_map = `false`
	)

inline

Explicit copy of graph.

This function takes a source graph gsrc for copying to to another target graph gtgt. First the function cleans gtgt; that is all its arc and nodes are removed and freed. Then gsrc is copyed to gtgt- The resulting gtgt is isomorphic to gsrc.

Eventually, the copy can be mapped through the cookies. For that, a forth bool parameter is specifyed-

Parameters

[in]	gsrc	source graph
[in]	gtgt	target graph
[in]	cookie_map	boolean indicating if the result must be mapped through the nodes and arcs cookies.

Exceptions

bad_alloc if there is no enough memory

Here is the call graph for this function:

Here is the caller graph for this function:

◆ depth_first_traversal()

template<class GT >

size_t Aleph::depth_first_traversal	(	const GT &	g,
		typename GT::Node *	start_node,
		bool()(const GT &g, typename GT::Node , typename GT::Arc *)	visit
	)

inline

Generic depth first traversal of a graph.

This function recursively traverses the graph g form start_node. On each node, a visit function is called, whose signature must match as follows:

bool visit(const GT & g, GT::Node * curr, GT::Arc * from)

g is the graph, curr is the currently visited node and from is the arc from whom curr was discovered. If visit returns false then the traversal continues; otherwise it stops.

The traversal uses the contro Depth_First

Parameters

[in]	g	the graph
[in]	start_node	the starting node
[in]	visit	function

Returns: the number of visited nodes

See also: breadth_first_traversal() test_connectivity()

◆ digraph_graphviz()

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >

void Aleph::digraph_graphviz	(	const GT &	g,
		std::ostream &	out,
		Node_Attr	node_attr = `Node_Attr()`,
		Arc_Attr	arc_attr = `Arc_Attr()`,
		const string &	rankdir = `"LR"`
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,output) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a output.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo
Node_Attr: genera la especifcaciÃ³n dot de un nodo
Arc_attr: genera la especifcaciÃ³n dot de un arco correspondiente al texto que se desea emitir.
SN: filtro para el iterador de nodos
SA: filtro para el iterador de arcos

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[out]	out	archivo hacia donde se emitirÃ¡ la salida.
[in]	rankdir	direcciÃ³n del dibujado entre los valores "TB", "BT", "LR" y "RL"

See also: Filter_Iterator

Here is the call graph for this function:

◆ edge_connectivity()

template<class GT , template< class > class Max_Flow = Random_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>

long Aleph::edge_connectivity ( GT & g )

Calcula la conectividad en arcos de un grafo.

edge_connectivity(g) calcula la conectividad en arcos de un grafo mediante maximizaciones sucesivas de flujo sobre una red alterna capacitada unitaria.

La rutina recibe dos parÃ¡etros tipo:

GT: el tipo grafo sobre al cual se le desea averiguar su conectividad.
Max_Flow el algoritmo de maximizaciÃ³n de flujo a emplear para averiguar conectividad.

Parameters

[in] g el grafo.

Returns: la conectividad en arcos del grafo g.

Exceptions

bad_alloc si no hay suficiente memoria.

Here is the call graph for this function:

◆ find_breadth_first_spanning_tree()

template<class GT >

GT Aleph::find_breadth_first_spanning_tree	(	GT &	g,
		typename GT::Node *	gp
	)

inline

Compute a breadth first ordered spanning tree starting from a specific node.

The returned spanning tree is mapped through the nodes and arcs cookies to teh original graph.

The function uses the control bit Spanning_Tree.

Note: If g is not connected then the spanning tree only will have the reachable nodes of the connected component where gnode is.

Parameters

[in]	g	the graph abarcador en profundidad.
[in]	gnode	source node in `g` from which to start the search

Returns: a spanning tree of g

Exceptions

bad_alloc if there is no enough memory

◆ find_depth_first_spanning_tree()

template<class GT >

GT Aleph::find_depth_first_spanning_tree	(	const GT &	g,
		typename GT::Node *	gnode
	)

inline

Compute a depth first ordered spanning tree starting from a specific node.

The returned spanning tree is mapped through the nodes and arcs cookies to teh original graph.

The function uses the control bit Spanning_Tree.

Note: If g is not connected then the spanning tree only will have the reachable nodes of the connected component where gnode is.

Parameters

[in]	g	the graph abarcador en profundidad.
[in]	gnode	source node in `g` from which to start the search

Returns: a spanning tree of g

Exceptions

bad_alloc if there is no enough memory

◆ find_min_path() [1/3]

template<class Mat >

void find_min_path	(	Mat &	p,
		const long &	src_idx,
		const long &	tgt_idx,
		Path< typename Mat::Graph_Type > &	path
	)

Construye un camino mÃnimo desde un nodo a otro a partir de una matriz de caminos calculada por el algoritmo de Floyd-Warshall.

Este procedimiento toma una matriz p que contiene los Ãndices de caminos mÃnimos calculados por el algoritmo de Floyd-Warshall, dos enteros i y j en la matriz correspondientes a los Ãndices del nodo origen y destino respectivamente, y calcula el camino mÃnimo en la representaciÃ³n con listas de adyacencia usada en el algoritmo de Floyd-Warshall.

Este procedimiento estÃ¡ concebido para llamarse despuÃ©s de ejecutar floyd_all_shortest_paths(), el cual calcula la matriz p.

Resultados son completamente indeterminados si la matriz p es invÃ¡lida.

Una versiÃ³n sobrecargada de este mÃ©todo toma como parÃ¡metros punteros a nodos, en lugar de Ãndices sobre la matriz.

Parameters

[in]	p	matriz de Ãndices de caminos mÃnimos.
[in]	src_idx	Ãndice del nodo origen dentro de la matriz de caminos mÃnimos.
[in]	tgt_idx	Ãndice del nodo destino dentro de la matriz de caminos mÃnimos.
[out]	path	el camino mÃnimo en el grafo representado con listas de adyacencia usado cuando se ejecutÃ³ floyd_all_shortest_paths().

Exceptions

bad_alloc si no hay suficiente memoria para construir el camino.

See also: floyd_all_shortest_paths()

Here is the call graph for this function:

Here is the caller graph for this function:

◆ find_min_path() [2/3]

template<class Mat >

void find_min_path	(	Mat &	p,
		typename Mat::Node *	src_node,
		typename Mat::Node *	tgt_node,
		Path< typename Mat::Graph_Type > &	path
	)

Construye un camino mÃnimo desde un nodo a otro a partir de una matriz de caminos calculada por el algoritmo de Floyd-Warshall.

Este procedimiento toma una matriz p que contiene los Ãndices de caminos mÃnimos calculados por el algoritmo de Floyd-Warshall, dos punteros correspondientes a los nodos origen y destino respectivamente en la representaciÃ³n con listas de adyacencia usada cuando se invocÃ³ a floyd_all_shortest_paths(), y calcula el camino mÃnimo.

Este procedimiento estÃ¡ concebido para llamarse despuÃ©s de ejecutar floyd_all_shortest_paths(), el cual calcula la matriz p.

Resultados son completamente indeterminados si la matriz p es invÃ¡lida.

Parameters

[in]	p	matriz de Ãndices de caminos mÃnimos.
[in]	src_node	puntero al nodo origen dentro de la representaciÃ³n con listas de adyacencia.
[in]	tgt_node	puntero al nodo destino dentro de la representaciÃ³n con listas de adyacencia.
[out]	path	el camino mÃnimo en el grafo representado con listas de adyacencia usado cuando se ejecutÃ³ floyd_all_shortest_paths().

Exceptions

bad_alloc si no hay suficiente memoria para construir el camino.

See also: floyd_all_shortest_paths()

Here is the call graph for this function:

◆ find_min_path() [3/3]

template<class Mat >

void find_min_path	(	Mat &	p,
		const long &	src_idx,
		const long &	tgt_idx,
		Path< typename Mat::Graph_Type > &	path
	)

Construye un camino mÃnimo desde un nodo a otro a partir de una matriz de caminos calculada por el algoritmo de Floyd-Warshall.

Este procedimiento toma una matriz p que contiene los Ãndices de caminos mÃnimos calculados por el algoritmo de Floyd-Warshall, dos enteros i y j en la matriz correspondientes a los Ãndices del nodo origen y destino respectivamente, y calcula el camino mÃnimo en la representaciÃ³n con listas de adyacencia usada en el algoritmo de Floyd-Warshall.

Este procedimiento estÃ¡ concebido para llamarse despuÃ©s de ejecutar floyd_all_shortest_paths(), el cual calcula la matriz p.

Resultados son completamente indeterminados si la matriz p es invÃ¡lida.

Una versiÃ³n sobrecargada de este mÃ©todo toma como parÃ¡metros punteros a nodos, en lugar de Ãndices sobre la matriz.

Parameters

[in]	p	matriz de Ãndices de caminos mÃnimos.
[in]	src_idx	Ãndice del nodo origen dentro de la matriz de caminos mÃnimos.
[in]	tgt_idx	Ãndice del nodo destino dentro de la matriz de caminos mÃnimos.
[out]	path	el camino mÃnimo en el grafo representado con listas de adyacencia usado cuando se ejecutÃ³ floyd_all_shortest_paths().

Exceptions

bad_alloc si no hay suficiente memoria para construir el camino.

See also: floyd_all_shortest_paths()

Here is the call graph for this function:

◆ find_path_breadth_first()

template<class GT >

Path<GT> Aleph::find_path_breadth_first	(	const GT &	g,
		typename GT::Node *	start,
		typename GT::Node *	end
	)

inline

Breadth first search of a path between two nodes.

find_path_breadth_first() searches in breadth first order a path between start_node y end_node

Parameters

[in]	g	the graph
[in]	start_node	pointer to starting node of search
[in]	end_node	pointer to ending node of search

Returns: a Path object containing the path if this was found; an empty path otherwise

Exceptions

bad_alloc if there is no enough memory

See also: find_path_breadth_first()

Here is the call graph for this function:

◆ find_path_depth_first()

template<class GT >

Path< GT > Aleph::Aleph::find_path_depth_first	(	const GT &	g,
		typename GT::Node *	start_node,
		typename GT::Node *	end_node
	)

inline

Depth first search of a path between two nodes.

find_path_depth_first() recursively searches a path between start_node y end_node

Parameters

[in]	g	the graph
[in]	start_node	pointer to starting node of search
[in]	end_node	pointer to ending node of search

Returns: a Path object containing the path if this was found; an empty path otherwise

Exceptions

bad_alloc if there is no enough memory

See also: find_path_breadth_first()

Here is the caller graph for this function:

◆ foldl_arcs() [1/2]

template<class GT , typename T , class SA = Dft_Show_Arc<GT>>

T Aleph::foldl_arcs	(	GT &	g,
		const T &	init,
		std::function< T(const T &, typename GT::Arc *)>	operation,
		SA	sa = `SA()`
	)

noexcept

Fold the filtered arcs of a graph.

Parameters

[in]	g	the graph
[in]	init	initial value of folded result
[in]	operation	folding operation on the arc
[in]	sa	arc filter

Returns: the final folded result

Here is the call graph for this function:

◆ foldl_arcs() [2/2]

template<class GT , typename T , class SA = Dft_Show_Arc<GT>>

T Aleph::foldl_arcs	(	GT &	g,
		typename GT::Node *	p,
		const T &	init,
		std::function< T(const T &, typename GT::Arc *)>	operation,
		SA	sa = `SA()`
	)

noexcept

Fold the filtered adjacent arcs of a node.

Parameters

[in]	g	the graph
[in]	p	node pointer
[in]	init	initial value of folded result
[in]	operation	folding operation on the arc
[in]	sa	arc filter

Returns: the final folded result

Here is the call graph for this function:

◆ foldl_nodes()

template<class GT , typename T , class SN = Dft_Show_Node<GT>>

T Aleph::foldl_nodes	(	GT &	g,
		const T &	init,
		std::function< T(const T &, typename GT::Node *)>	operation,
		SN	sn = `SN()`
	)

noexcept

Fold the filtered nodes of a graph.

Parameters

[in]	g	the graph
[in]	init	initial value of folded result
[in]	operation	folding operation on the node
[in]	sn	node filter

Returns: the final folded result

Here is the call graph for this function:

◆ for_each_arc() [1/3]

template<class GT , class SA = Dft_Show_Arc<GT>>

void Aleph::for_each_arc	(	const GT &	g,
		std::function< void(typename GT::Arc *)>	operation,
		SA	sa = `SA()`
	)

noexcept

Traverse all the arcs of graph filtering some ones according to a condition and executing an operation on them.

Parameters

[in]	g	the graph
[in]	operation	to be executed on each seen arc
[in]	sa	an arc filter

Here is the caller graph for this function:

◆ for_each_arc() [2/3]

template<class GT , class SA = Dft_Show_Arc<GT>>

void Aleph::for_each_arc	(	const GT &	,
		typename GT::Node *	p,
		std::function< void(typename GT::Arc *)>	operation,
		SA	sa = `SA()`
	)

noexcept

Traverse all the arcs adjacent to a node filtering some ones according to a condition and executing an operation on them.

Parameters

[in]	g	the graph
[in]	p	a node pointer
[in]	operation	to be executed on each seen arc
[in]	sa	an arc filter

◆ for_each_arc() [3/3]

template<class GT , class Itor , class Operation >

void Aleph::for_each_arc	(	typename GT::Node *	p,
		Operation	op = `Operation()`
	)

inlinenoexcept

Execute an operation on each arc of a node.

This template function receives threes template parameters:

GT: the graph type.
Itor: the iterator type; it is intended to be __In_Iterator or __Out_Iterator.
Operation: an operation to be executed on each arc. This operation must have the following signature:
```
void operation(typename GT::Arc * arc)
```

Parameters

[in]	p	node pointer
[in]	operation	to be performed on each arc

Here is the caller graph for this function:

◆ for_each_in_arc()

template<class GT , class Op >

void Aleph::for_each_in_arc	(	typename GT::Node *	p,
		Op	op = `Op()`
	)

inlinenoexcept

Traverse the incoming arcs of a node and executes an operation

Parameters

[in]	p	node pointer
[in]	op	operation to perform on each node

Here is the call graph for this function:

Here is the caller graph for this function:

◆ for_each_node()

template<class GT , class SN = Dft_Show_Node<GT>>

void Aleph::for_each_node	(	const GT &	g,
		std::function< void(typename GT::Node *)>	operation,
		SN	sn = `SN()`
	)

noexcept

Traverse all the nodes of graph filtering some ones according to a condition and executing an operation on them.

Parameters

[in]	g	the graph
[in]	operation	to be executed on each seen node
[in]	sn	a node filter

Here is the caller graph for this function:

◆ for_each_out_arc()

template<class GT , class Op >

void Aleph::for_each_out_arc	(	typename GT::Node *	p,
		Op	op = `Op()`
	)

inlinenoexcept

Traverse the outcoming arcs of a node and executes an operation

Parameters

[in]	p	node pointer
[in]	op	operation to perform on each node

Here is the call graph for this function:

Here is the caller graph for this function:

◆ forall_arc() [1/2]

template<class GT , class SA = Dft_Show_Arc<GT>>

bool Aleph::forall_arc	(	const GT &	g,
		std::function< bool(typename GT::Arc *)>	cond,
		SA	sa = `SA()`
	)

noexcept

Return true if condition cond is met on every filtered arc of the graph.

Parameters

[in]	g	the graph
[in]	cond	condition
[in]	sa	arc filter

Returns: true if all the arcs satisfy the condition; false otherwise

◆ forall_arc() [2/2]

template<class GT , class SA = Dft_Show_Arc<GT>>

bool Aleph::forall_arc	(	typename GT::Node *	p,
		std::function< bool(typename GT::Arc *)>	cond,
		SA	sa = `SA()`
	)

noexcept

Return true if condition cond is met on every filtered arc of a node.

Parameters

[in]	p	node pointer
[in]	cond	condition
[in]	sa	arc filter

Returns: true if all the arcs satisfy the condition; false otherwise

◆ forall_node()

template<class GT , class SN = Dft_Show_Node<GT>>

bool Aleph::forall_node	(	const GT &	g,
		std::function< bool(typename GT::Node *)>	cond,
		SN	sn = `SN()`
	)

noexcept

Return true if condition cond is met on every filtered node of the graph.

Parameters

[in]	g	the graph
[in]	cond	condition
[in]	sn	node filter

Returns: true if all the nodes satisfy the conition; false otherwise

◆ generate_cross_graph()

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >

void Aleph::generate_cross_graph	(	GT &	g,
		const size_t &	nodes_by_level,
		const double &	xdist,
		const double &	ydist,
		std::ostream &	out
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,out) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a out.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo.
SA: clase filtro de arcos.
Write_Node: convierte el contenido de un nodo a un string correspondiente al texto que se desea emitir.
Write_Arc: convierte el contenido de un arco a un string correspondiente al texto que se desea emitir.
Shade_Node: comando a emitir para un nodo oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Node).
Shade_Arc: comando a emitir para un arco oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Arc.

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[in]	nodes_by_level	cantidad de nodos por nivel. El nÃºmero de nodos del Ãºltimo nivel dependerÃ¡ de la cantidad de nodos que contenga el grafo.
[in]	xdist	separaciÃ³n horizontal entre los nodos.
[in]	ydist	separaciÃ³n vertical entre los nodos.
[out]	out	archivo hacia donde se emitirÃ¡ la salida.

Here is the caller graph for this function:

◆ generate_graphpic()

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >

void Aleph::generate_graphpic	(	const GT &	g,
		const double &	xdist,
		const double &	,
		std::ostream &	output
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,output) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a output.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo.
SA: clase filtro de arcos.
Write_Node: convierte el contenido de un nodo a un string correspondiente al texto que se desea emitir.
Write_Arc: convierte el contenido de un arco a un string correspondiente al texto que se desea emitir.
Shade_Node: comando a emitir para un nodo oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Node).
Shade_Arc: comando a emitir para un arco oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Arc.
SA: filtro para el iterador de arcos

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[in]	xdist	separaciÃ³n horizontal entre los nodos.
[out]	output	archivo hacia donde se emitirÃ¡ la salida.

See also: Filter_Iterator

◆ generate_graphviz() [1/2]

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class Dashed_Node , class Dashed_Arc , class SA , class SN >

void Aleph::generate_graphviz	(	const GT &	g,
		std::ostream &	output,
		const string &	rankdir = `"TB"`,
		float	ranksep = `0.2`,
		float	nodesep = `0.2`
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,output) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a output.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo.
Write_Node: convierte el contenido de un nodo a un string correspondiente al texto que se desea emitir.
Write_Arc: convierte el contenido de un arco a un string correspondiente al texto que se desea emitir.
Shade_Node: comando a emitir para un nodo oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa.
Shade_Arc: comando a emitir para un arco oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa.
Dashed_Node: comando para generar lÃnea del nodo punteada.
Dashed_Arc: comando para generar lÃnea del arco punteada.
SA: filtro para el iterador de arcos.
SN: filtro para el iterador de nodos.

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[out]	output	archivo hacia donde se emitirÃ¡ la salida.
[in]	rankdir	direcciÃ³n del dibujado entre los valores "TB", "BT", "LR" y "RL"
[in]	ranksep	separaciÃ³n entre rangos topolÃ³gicos (cuando aplique)
[in]	nodesep	separaciÃ³n entre los nodos

See also: Filter_Iterator

◆ generate_graphviz() [2/2]

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >

void Aleph::generate_graphviz	(	const GT &	g,
		std::ostream &	out,
		Node_Attr	node_attr = `Node_Attr()`,
		Arc_Attr	arc_attr = `Arc_Attr()`,
		const string &	rankdir = `"TB"`
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,output) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a output.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo
Node_Attr: genera la especifcaciÃ³n dot de un nodo
Arc_attr: genera la especifcaciÃ³n dot de un arco correspondiente al texto que se desea emitir.
SN: filtro para el iterador de nodos
SA: filtro para el iterador de arcos

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[out]	out	archivo hacia donde se emitirÃ¡ la salida.
[in]	rankdir	direcciÃ³n del dibujado entre los valores "TB", "BT", "LR" y "RL"

See also: Filter_Iterator

Here is the caller graph for this function:

◆ generate_net_graph()

template<class GT , class Write_Node , class Write_Arc , class Shade_Node , class Shade_Arc , class SA >

void Aleph::generate_net_graph	(	GT &	g,
		const size_t &	nodes_by_level,
		const double &	xdist,
		const double &	ydist,
		std::ostream &	out
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo red.

En un dibujo de red, siempre se distribuyen nodes_by_level nodos por nivel.

generate_net_graph(g,nodes_by_level,xdist,ydist,out) genera una entrada a graphpic de un grafo red de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a out.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo.
SA: clase filtro de arcos.
Write_Node: convierte el contenido de un nodo a un string correspondiente al texto que se desea emitir.
Write_Arc: convierte el contenido de un arco a un string correspondiente al texto que se desea emitir.
Shade_Node: comando a emitir para un nodo oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Node.
Shade_Arc: comando a emitir para un arco oscuro. Si no se desea oscurecer, entonces se debe generar la cadena vacÃa; de lo contrario, generar el comando graphpic (por lo general Shadow-Arc.

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[in]	nodes_by_level	cantidad de nodos por nivel. El nÃºmero de nodos del Ãºltimo nivel dependerÃ¡ de la cantidad de nodos que contenga el grafo.
[in]	xdist	separaciÃ³n horizontal entre los nodos.
[in]	ydist	separaciÃ³n vertical entre los nodos.
[out]	out	archivo hacia donde se emitirÃ¡ la salida.

Here is the call graph for this function:

◆ graph_to_tree_node()

template<class GT , typename Key , class Convert , class SA = Dft_Show_Arc<GT>>

Tree_Node<Key>* Aleph::graph_to_tree_node	(	GT &	g,
		typename GT::Node *	groot
	)

inline

Convierte un Ã¡rbol representado en una representaciÃ³n de grafo a un Ã¡rbol Tree_Node.

graph_to_tree_node() toma un Ã¡rbol representado mediante algÃºn tipo de grafo representado con listas de adyacencia y un nodo groot que se asume raÃz del Ã¡rbol y lo convierte a un Ã¡rbol representado con el tipo Tree_Node<Key>.

El interÃ©s de esta rutina es obtener una representaciÃ³n del Ã¡rbol en la cual se puedan aplicar otras tÃ©cnicas, clases y algoritmos. Un ejemplo representativo es el dibujado de Ã¡rboles inherentes a los grafos; en la ocurrencia, Ã¡rboles abarcadores.

El procedimiento utiliza el bit spanning_tree para marcar los nodos y arcos ya visitados.

Como medio de representaciÃ³n, el tipo Tree_Node<Key> es menos versÃ¡til que cualquier tipo basado en un grafo representado con listas de adyacencia; por ejemplo, List_graph. Note, por instancia, que List_Graph<Node,Arc> estipula un tipo para los arcos, mientras que no ocurre lo mismo para Tree_Node<Key>. En este sentido, como representaciÃ³n, Tree_Node<Key> no tiene ningÃºn medio para guardar los datos asociados a los arcos. Consecuentemente, sÃ³lo se podrÃa manejar los datos contenidos en los nodos. Por otra parte, el tipo guardado en GT::Node puede ser de Ãndole distinta al guardado en Tree_Node<Key>.

A menudo (ese es el caso tÃpico del dibujado), el tipo de dato a guardar en Tree_Node<Key> es de Ãndole distinta al guardado en GT::Node. Otras veces, lo que se desea guardar en cada Tree_Node<Key> es un subconjunto de lo que estÃ¡ guardado en GT::Node. Puesto que es imposible generizar todos los casos posibles, la escritura de cada Tree_Node<Key> se delega a una clase cuyo operador ()() es invocado por la rutina de conversiÃ³n para cada nodo del grafo. La clase en cuestiÃ³n es el parÃ¡metro tipo Convert.

La clase Convert se invoca de la siguiente manera:

void Convert::operator () (gnode, tnode)

donde:
-# gnode es de tipo GT::Node
-# tnode de tipo Tree_Node<Key>

La rutina hace una prueba de aciclicidad sobre g mediante la funciÃ³n is_graph_acyclique(), lo que no afecta la complejidad algorÃtmica de pero que toma tiempo adicional.

El procedimiento maneja los siguientes tipos parametrizados:

GT: el tipo de grafo, el cual debe ser derivado de List_Graph.
Key: el tipo de dato que albergarÃ¡ el Ã¡rbol en su representaciÃ³n Tree_Node<Key>.
Convert: clase de conversiÃ³n de GT::Node a Key, cuyo operador ()(gnode,tnode) es invocado por cada nodo de g cuando se realiza la conversiÃ³n a uno Tree_Node.
SA: filtro de arcos.

Parameters

[in]	g	el Ã¡rbol de tipo GT (derivado de List_Graph) que se desea convertir.
[in]	groot	el nodo de g que se considera raÃz del Ã¡rbol.

Returns: la raÃz de un Ã¡rbol de tipo Tree_Node<Key> correspondiente a la conversiÃ³n

Exceptions

bad_alloc si no hay memoria para apartar el Ã¡rbol de tipo Tree_Node<Key>

See also: Tree_Node is_graph_acyclique()

◆ in_arcs()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<typename GT::Arc*> Aleph::in_arcs	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the filtered incoming arcs of p.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Here is the call graph for this function:

Here is the caller graph for this function:

◆ in_degree()

template<class GT , class SA = Dft_Show_Arc<GT>>

size_t Aleph::in_degree	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Compute the filtered in degree of node p.

Note: This function computes the degree, it does not retrieve it.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Returns: the incoming degree

Here is the caller graph for this function:

◆ in_nodes()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<typename GT::Node*> Aleph::in_nodes	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the nodes connected to the filtered incoming arcs to p.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Returns: A DynList<typename GT::Node*> with the pointer to the incoming nodes

Here is the call graph for this function:

Here is the caller graph for this function:

◆ in_pairs()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<ArcPair<GT> > Aleph::in_pairs	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the filtered incoming pairs of (arc,node) related to node p

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Here is the call graph for this function:

◆ inconnected_components()

template<class GT >

DynList< GT > Aleph::Aleph::inconnected_components ( const GT & g )

inline

Compute a list of subgraphs corresponding to the inconnected component of a graph.

After completion, the subgraphs are mapped through the nodes and arcs cookies to the original graph.

This function uses the control bit Build_Subtree.

The algorithm user depth first search and takes 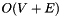$O(V + E)$ in complexity.

Parameters

[in] g the graph

Returns: a list of mapped graphs corresponding to the connected components of g

Exceptions

bad_alloc if there is no enough memory

See also: copy_graph()

◆ inter_copy_graph()

template<class GTT , class GTS , class Copy_Node = Dft_Copy_Node<GTT, GTS>, class Copy_Arc = Dft_Copy_Arc<GTT, GTS>>

void Aleph::inter_copy_graph	(	GTT &	gtgt,
		const GTS &	gsrc,
		const bool	cookie_map = `false`
	)

Copy between different types of graphs.

Parameters

[in]	gtgt	target graph
[in]	gsrc	source graph
[in]	cookie_map	if `true` ==> a mapping will be done through nodes and arcs cookies

Here is the call graph for this function:

◆ invert_digraph()

template<class GT >

GT Aleph::invert_digraph ( const GT & g )

Compute the inverted graph; that is the seame nodes but its arcs inverted.

After call the graphs are mapped.

Parameters

[in] g the graph

Returns: a inverted a mapped graph to g

Exceptions

bad_alloc if there is no enough memory

Here is the call graph for this function:

Here is the caller graph for this function:

◆ kosaraju_connected_components() [1/2]

template<class GT >

void Aleph::kosaraju_connected_components	(	const GT &	g,
		DynList< GT > &	blk_list,
		DynList< typename GT::Arc *> &	arc_list
	)

inline

Calcula los componentes fuertemente conexos de un grafo segÃºn el algoritmo de Kosaraju.

kosaraju_connected_components() toma un digrafo g, "supuestamente dÃ©bilmente conexo", calcula sus subgrafos o componentes inconexos y los almacena en una lista dinÃ¡mica list de subdigrafos mapeados, tanto en los nodos como en los arcos. El Ã©nfasis en el supuesto carÃ¡cter conexo del grafo se debe a que si el grafo no fuese conexo, entonces la lista resultante contendrÃa un solo elemento correspondiente al digrafo copia mapeado de g. Si este fuese el caso, entonces es preferible hacerlo con la funciÃ³n copy_graph().

La funciÃ³n se basa en el algoritmo de Tarjan.

La funciÃ³n emplea dos parÃ¡metros tipo:

GT: la clase digrafo.
SA: el filtro de arcos que emplea el iterador interno.

La funciÃ³n se vale del bit build_subtree para marcar nodos y arcos visitados.

El algoritmo internamente descubre los componentes mediante bÃºsquedas en profundidad.

Parameters

[in]	g	el grafo.
[out]	blk_list	lista de sub-grafos mapeados a g correspondiente a los componentes fuertemente conexos de g.
[out]	arc_list	lista de arcos de cruce entre los componentes.

See also: tarjan_connected_components()

Here is the call graph for this function:

◆ kosaraju_connected_components() [2/2]

template<class GT >

DynList<DynList<typename GT::Node*> > Aleph::kosaraju_connected_components ( const GT & g )

inline

Calcula los componentes fuertemente conexos de un grafo segÃºn el algoritmo de Kosaraju.

kosaraju_connected_components() toma un digrafo g, "supuestamente dÃ©bilmente conexo", calcula sus subgrafos o componentes inconexos y los almacena en una lista dinÃ¡mica list de subdigrafos mapeados, tanto en los nodos como en los arcos. El Ã©nfasis en el supuesto carÃ¡cter conexo del grafo se debe a que si el grafo no fuese conexo, entonces la lista resultante contendrÃa un solo elemento correspondiente al digrafo copia mapeado de g. Si este fuese el caso, entonces es preferible hacerlo con la funciÃ³n copy_graph().

La funciÃ³n se basa en el algoritmo de Kosaraju, el cual no es el mÃ¡s eficiente conocido pero sÃ es el mÃ¡s simple.

La funciÃ³n emplea dos parÃ¡metros tipo:

GT: la clase digrafo.
SA: el filtro de arcos que emplea el iterador interno.

La funciÃ³n se vale del bit build_subtree para marcar nodos y arcos visitados.

El algoritmo internamente descubre los componentes mediante bÃºsquedas en profundidad.

La diferencia y ventaja de esta rutina respecto a la versiÃ²n que calcula los bloques directos es su rapidez; los bloque son comprendidos en listas de listas de nodos y no en lista de subgrafos.

Parameters

[in]	g	el grafo.
[out]	list	lista de listas de nodos que conforman los componentes. Cada lista es una listas de los nodos del componente.

See also: tarjan_connected_components()

Here is the call graph for this function:

◆ map_arcs()

template<class GTS , class GTT >

void Aleph::map_arcs	(	typename GTS::Arc *	p,
		typename GTT::Arc *	q
	)

noexcept

Map two arcs of different types of graphs through their cookies

Note: It is intended that the mapping be done between at least homomorphic graphs

Parameters

[in]	p	pointer to the source arc
[in]	q	pointer to the target arc

Here is the caller graph for this function:

◆ map_cut_graph()

template<class GT >

std::tuple<GT, DynList<typename GT::Arc*> > Aleph::map_cut_graph	(	const GT &	g,
		const DynList< typename GT::Node *> &	cut_node_list
	)

Extract a mapped copy of cut graph.

map_cut_graph(g, cut_node_list) extracts, according to cut_node_list, the cut graph.

The cut graph is composed by the cut nodes and arcs. A cut arc if an arc linking two cut points.

An arc linking a cut point with a non cut point is called a "cross arc".

The function requires that nodes and arcs are marked with their respective control bits as well as they are painted. So, this requires that the cut points has previously been computed and the graph has been painted.

Parameters

[in]	g	the graph
[in]	cut_node_list	list with the cut points grafo es a menudo inconexo.

Returns: a tuple<GT, DynList<typename GT::Arc*>> whose first element is the cut graph and the second is a list with the cross arcs.

Exceptions

bad_alloc if there is no enough memory

See also: map_subgraph() compute_cut_nodes() paint_subgraphs()

Here is the call graph for this function:

◆ map_nodes()

template<class GTS , class GTT >

void Aleph::map_nodes	(	typename GTS::Node *	p,
		typename GTT::Node *	q
	)

noexcept

Map two nodes of different types of graphs through their cookies

Note: It is intended that the mapping be done between at least homomorphic graphs

Parameters

[in]	p	pointer to the source node
[in]	q	pointer to the target node

Here is the caller graph for this function:

◆ map_subgraph()

template<class GT >

GT Aleph::map_subgraph	(	const GT &	g,
		const long	color
	)

Extract a mapped copy of a subgraph with a specific color.

map_subgraph(g, color) searches a node of g with the color. Once found, the graph is traversed in depth first order and all the nodes and arcs with color are copied and mapped to a resulting subgraph.

map_subgraph() was/is primarily destined to extract a block according to a cut point and paint_subgraphs(). However, this function could perfectly be used for extracting any painted subgraph.

Parameters

[in]	g	the graph
[in]	color	the color value

Returns: a mapped subgraph whose nodes and arcs have te color

Exceptions

bad_alloc if there is no enough memory

See also: paint_subgraphs() compute_cut_nodes() map_cut_graph()

Here is the call graph for this function:

◆ mapped_node()

template<class GT >

GT::Node* Aleph::mapped_node ( typename GT::Node * p )

noexcept

Return the mapped node through the cookie of p

Here is the call graph for this function:

◆ nodes_map()

template<class GT , typename T , template< typename > class Container = DynList, class SN = Dft_Show_Node<GT>>

Container<T> Aleph::nodes_map	(	GT &	g,
		std::function< T(typename GT::Node *)>	transformation,
		SN	sn = `SN()`
	)

Map the filtered nodes of a graph to a transformed type.

Parameters

[in]	g	the grapg
[in]	transformation	function `Node*` –> T`
[in]	sn	node filter

Returns: a Container<T> object with all the nodes mapped through the transformation

◆ out_arcs()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<typename GT::Arc*> Aleph::out_arcs	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the filtered incoming arcs of p.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Here is the call graph for this function:

◆ out_degree()

template<class GT , class SA = Dft_Show_Arc<GT>>

size_t Aleph::out_degree	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Compute the filtered out degree of node p

Note: This function computes the degree, it does not retrieve it.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Returns: the outcoming degree

Here is the caller graph for this function:

◆ out_nodes()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<typename GT::Node*> Aleph::out_nodes	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the nodes connected to the filtered outcoming arcs of p.

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Returns: A DynList<typename GT::Node*> with the pointer to the outcoming nodes

Here is the call graph for this function:

Here is the caller graph for this function:

◆ out_pairs()

template<class GT , class SA = Dft_Show_Arc<GT>>

DynList<ArcPair<GT> > Aleph::out_pairs	(	typename GT::Node *	p,
		SA	sa = `SA()`
	)

Return the filtered outcoming pairs of (arc,node) related to node p

Parameters

[in]	p	node pointer
[in]	sa	arc filter

Returns: a DynList<ArcPair<GT>> containg the outcoming pairs

Here is the call graph for this function:

◆ paint_subgraphs()

template<class GT >

long Aleph::paint_subgraphs	(	const GT &	g,
		const DynList< typename GT::Node *> &	cut_node_list
	)

inline

Paint a connected graph according to its cut points.

paint_subgraphs() takes a graph and a cut points list previously computed with compute_cut_nodes() and on the graph paints its nodes and arcs witg different colors according to the cut points. The color would allow to distinguish the components which are separated by cut points. The color is defined with the counter attribute of node and arcs.

The first color starts from one. The number of color is thus the number of different components.

paint_subgraphs() uses the control bit Cut in order to differentiate the cut nodes and arcs. So, the graph must remain intact after the cut nodes computation. The procedure internally uses also the control bit Build_Subtree.

Note: In order to this function works you must strictly respect the protocol. That is, you call to compute_cut_nodes(), whick gives the cut nodes list and leaves the nodes and arcs of the graph adequately marked. You must not alter the control bits of graph. cruce (arcos adyacentes a un punto de corte). If this protocol is respected, the this fuction will not fail, because it does not require memory.

Parameters

[in]	g	the grapg to be painted
[in]	cut_node_list	cut nodes list previously computed with `compute_cut_node()`

Returns: the number of colors which is exactly the number of component separated by the cut cpoints

See also: compute_cut_nodes() map_subgraph() map_cut_graph()

Here is the call graph for this function:

◆ rank_graphviz()

template<class GT , class Node_Attr , class Arc_Attr , class SN , class SA >

size_t Aleph::rank_graphviz	(	const GT &	g,
		std::ostream &	out,
		Node_Attr	node_attr = `Node_Attr()`,
		Arc_Attr	arc_attr = `Arc_Attr()`,
		const string &	rankdir = `"LR"`
	)

Genera una especificaciÃ³n para el programa de dibujado de grafos graphpic de tipo grafo cruzado.

En un dibujo de grafo cruzado, se distribuyen nodes_by_level - 1 nodos los niveles pares y num_nodes_by_level en los impares.

generate_cross_graph(g,nodes_by_level,xdist,ydist,output) genera una entrada a graphpic de un grafo cruzado de nodes_by_level, separados horizontalmente por xdist y verticalmente por ydist. La salida se emite al archivo asociado a output.

Para tratar con los contenidos de los nodos y arcos y lo que se desee generar, se emplean los siguientes parÃ¡metros tipo:

GT: el tipo de grafo o digrafo
Node_Attr: genera la especifcaciÃ³n dot de un nodo
Arc_attr: genera la especifcaciÃ³n dot de un arco correspondiente al texto que se desea emitir.
SN: filtro para el iterador de nodos
SA: filtro para el iterador de arcos

Parameters

[in]	g	grafo o digrafo del que se desea generar el dibujo.
[out]	out	archivo hacia donde se emitirÃ¡ la salida.
[in]	rankdir	direcciÃ³n del dibujado entre los valores "TB", "BT", "LR" y "RL"

See also: Filter_Iterator

Here is the call graph for this function:

◆ search_arc()

template<class GT , class SA = Dft_Show_Arc<GT>>

GT::Arc* Aleph::search_arc	(	const GT &	g,
		typename GT::Node *	src,
		typename GT::Node *	tgt,
		SA	sa = `SA()`
	)

noexcept

Arc filtered searching given two nodes.

This function receives two nodes and returns the first arc linking them. The arc sense is irrelevant for this function. Simply, it searches an arc linking the nodes

Parameters

[in]	g	the graph
[in]	src	a node
[in]	tgt	another node
[in]	sa	filtering condition

Returns: pointer to found node; nullptr otherwise

Here is the caller graph for this function:

◆ search_directed_arc()

template<class GT , class SA = Dft_Show_Arc<GT>>

GT::Arc* Aleph::search_directed_arc	(	const GT &	,
		typename GT::Node *	src,
		typename GT::Node *	tgt,
		SA	sa = `SA()`
	)

noexcept

Searching of directed arc linking two nodes.

Parameters

[in]	g	the graph
[in]	src	source node pointer
[in]	tgt	target node pointer

Returns: a pointer to a directed linking arc if this is found; nullptr otherwise.

Here is the caller graph for this function:

◆ sufficient_hamiltonian() [1/2]

template<class GT , class Init_Node , class Init_Arc >

GT Aleph::Random_Graph_Base< GT, Init_Node, Init_Arc >::sufficient_hamiltonian	(	const size_t &	__num_nodes,
		const double &	p = `0.5`
	)

inline

Crea un grafo aleatorio hamiltoniano.

Esta versiÃ³n construye un grafo aleatorio hamiltoniano.

El proceso primero genera un grafo aleatorio, luego examina el grafo resultante y crea nuevos arcos de modo que el resultado contenga un ciclo hamiltoniano.

Warning: El procedimiento puede ser extremadamente lento y goloso en memoria conforme aumente el valor de __num_nodes.; El grafo se asegura a ser hamiltoniano por los teoremas de Ore y Dirac. En este sentido, nÃ³tese que que la condiciÃ³n de hamiltoniano es de suficiencia, lo cual significa que no se trata de un grafo mÃnimo. De hecho, el grafo generado tiende a ser denso.

Parameters

[in]	__num_nodes	cantidad de nodos que debe tener el grafo.
[in]	p	probabilidad de existencia de arco entre cualquier par de nodos. Por omisiÃ³n este parÃ¡metro tiene valor 0.5, valor que intuitiva y empÃricamente tiende a generar menor arcos y consumir menos tiempo.

Returns: puntero al grafo aleatorio creado.

Exceptions

bad_alloc	si no hay suficiente memoria.
domain_error	si el valor de p no estÃ¡ entre 0 y 1.

◆ sufficient_hamiltonian() [2/2]

template<class GT, class Init_Node = Dft_Init_Rand_Node<GT>, class Init_Arc = Dft_Init_Rand_Arc<GT>>

GT Aleph::Random_Graph< GT, Init_Node, Init_Arc >::sufficient_hamiltonian	(	const size_t &	__num_nodes,
		const double &	p = `0.5`
	)

inline

Crea un grafo aleatorio hamiltoniano.

Esta versiÃ³n construye un grafo aleatorio hamiltoniano.

El proceso primero genera un grafo aleatorio, luego examina el grafo resultante y crea nuevos arcos de modo que el resultado contenga un ciclo hamiltoniano.

Warning: El procedimiento puede ser extremadamente lento y goloso en memoria conforme aumente el valor de __num_nodes.; El grafo se asegura a ser hamiltoniano por los teoremas de Ore y Dirac. En este sentido, nÃ³tese que que la condiciÃ³n de hamiltoniano es de suficiencia, lo cual significa que no se trata de un grafo mÃnimo. De hecho, el grafo generado tiende a ser denso.

Parameters

[in]	__num_nodes	cantidad de nodos que debe tener el grafo.
[in]	p	probabilidad de existencia de arco entre cualquier par de nodos. Por omisiÃ³n este parÃ¡metro tiene valor 0.5, valor que intuitiva y empÃricamente tiende a generar menor arcos y consumir menos tiempo.

Returns: puntero al grafo aleatorio creado.

Exceptions

bad_alloc	si no hay suficiente memoria.
domain_error	si el valor de p no estÃ¡ entre 0 y 1.

Here is the call graph for this function:

◆ test_connectivity()

template<class GT >

bool Aleph::test_connectivity ( const GT & g )

inline

Simple connectivity test.

Parameters

[in] g a graph

Returns: true if g is connected

Note: This function does not work for multigraphs

Exceptions

domain_error if g is a directed graph

See also: depth_first_traversal() is_reachable()

◆ test_for_cycle()

template<class GT >

bool Aleph::test_for_cycle	(	const GT &	g,
		typename GT::Node *	src
	)

inline

Single cycle searching from a node.

test_for_cycle(g, src) perform a depth first traversal on graph g searching a cycle starting from node src.

The control bit Test_Cycle is used.

Note: This function only test for a cycle starting from src. It takes for the worst case. If your goal simply is to determine whether the graph has or not cycles, then this is not the appropiate way. Use has_cycle() instead, which is 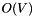for worst case.

Parameters

[in]	g	the graph
[in]	src	pointer to node

Returns: true if there is a cycle from src

See also: has_cycle() is_graph_acyclique()

◆ test_for_path()

template<class GT >

bool Aleph::test_for_path	(	const GT &	g,
		typename GT::Node *	start_node,
		typename GT::Node *	end_node
	)

inline

Test for path between two nodes.

The contros Bit Test_path is used.

The function is 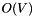$O(V)$ worst case

Parameters

[in]	g	the graph
[in]	start_node	pointer to start node
[in]	end_node	pointer to end node

Returns: true if it exists a path between start_node and end_node

See also: find_path_depth_first() find_path_breadth_first()

◆ traverse_arcs()

template<class GT , class Itor , class Operation >

bool Aleph::traverse_arcs	(	typename GT::Node *	p,
		Operation	op = `Operation()`
	)

inlinenoexcept

Generic arcs traverse of a node.

This template function receives threes template parameters:

GT: the graph type.
Itor: the iterator type; it is intended to be __In_Iterator or __Out_Iterator.
Operation: an operation to be executed on each arc. This operation must have the following signature:
```
bool operation(typename GT::Arc * arc)
```
If operation returns true then the traversal continues to the next arc; otherwise the traversal stops and the result of traverse() is false. If all the arcs are traversed, then the result is true.

Parameters

[in]	p	node pointer
[in]	operation	to be performed on each arc

Returns: true if all the arcs were traversed: false otherwise

Here is the caller graph for this function:

◆ traverse_in_arcs()

template<class GT , class Op >

bool Aleph::traverse_in_arcs	(	typename GT::Node *	p,
		Op	op = `Op()`
	)

inlinenoexcept

Conditioned traversal of incoming arcs of a node.

Parameters

[in]	p	node pointer
[in]	op	operation whose result must be `bool`. Si the result is `false`, then the traversal stops and the traverse returns `false`; otherwise, all the ars are traversed and it returns `true`

Returns: true is all the arcs were traversed: false otherwise

Here is the caller graph for this function:

◆ traverse_out_arcs()

template<class GT , class Op >

bool Aleph::traverse_out_arcs	(	typename GT::Node *	p,
		Op	op = `Op()`
	)

inlinenoexcept

Conditioned traversal of outcoming arcs of a node.

Parameters

[in]	p	node pointer
[in]	op	operation whose result must be `bool`. Si the result is `false`, then the traversal stops and the traverse returns `false`; otherwise, all the ars are traversed and it returns `true`

Returns: true is all the arcs were traversed: false otherwise

Here is the caller graph for this function:

◆ vertex_connectivity()

template<class GT , template< class > class Max_Flow = Random_Preflow_Maximum_Flow, class SA = Dft_Show_Arc<GT>>

long Aleph::vertex_connectivity ( GT & g )

Esta rutina se vale de un algoritmo de maximizaciÃ³n de flujo para calcular la conectividad en nodos de un grafo. Como tal, su segundo parÃ¡metro plantilla es el algoritmo de maximizaciÃ³n de flujo.

Parameters

[in] g el grafo.

Here is the call graph for this function:

◆ warshall_compute_transitive_clausure()

template<class GT , class SA = Dft_Show_Arc<GT>>

void Aleph::warshall_compute_transitive_clausure	(	GT &	g,
		Bit_Mat_Graph< GT, SA > &	mat
	)

CÃ¡lculo de la clausura transitiva de una matriz de adyacencia.

Esta funciÃ³n calcula la clausura transitiva del grafo g mediante el algoritmo de Warshall. El resultado se almacena en la matriz de bits mat.

Cada entrada mat(i,j) indica existencia de un camino entre el nodo origen con Ãndice i y el nodo destino con Ãndice j. Un valor cero indica que no hay ningÃºn camino; un valor 1 que existe al menos un camino.

El procedimiento utiliza dos matrices de bits; una de uso interno que es liberada al tÃ©rmino del procedimiento y la propia matriz mat.

Parameters

[in]	g	el grafo representado mediante una variante de List_Graph.
[out]	mat	matriz de bits donde se coloca el resultado.

Exceptions

bad_alloc si no hay suficiente memoria.

See also: List_Graph Bit_Mat_Graph

Here is the call graph for this function:

Variable Documentation

◆ Processed

const unsigned char Aleph::Processed

The node or arc has already been processed

◆ Processing

const unsigned char Aleph::Processing

The node are being processed; probably it is inside a queue, stack or heap

◆ Unprocessed

const unsigned char Aleph::Unprocessed

The node have not bees processed. This must be the initial state before general processing

Classes

Macros

Typedefs

Enumerations

Functions

Variables

Detailed Description

Introduction

Specifiying a graph

Specifiying the node

Specifiying the arc

Specifying the Graph

Filtered iterators

Un brief example

Convention about filtered iterators

When to use then?

Macro Definition Documentation

◆ ARC_BITS

◆ ARC_COLOR

◆ ARC_COOKIE

◆ ARC_COUNTER

◆ IS_ARC_VISITED

◆ IS_NODE_VISITED

◆ NODE_BITS

◆ NODE_COLOR

◆ NODE_COOKIE

◆ NODE_COUNTER

Typedef Documentation

◆ __In_Iterator

◆ __Out_Iterator

◆ ArcPair

Enumeration Type Documentation

◆ Graph_Bits

Function Documentation

◆ arcs()

◆ arcs_map() [1/2]

◆ arcs_map() [2/2]

◆ breadth_first_traversal()

◆ build_spanning_tree()

◆ build_subgraph()

◆ clear_graph()

◆ compute_bipartite()

◆ compute_cut_nodes()

◆ compute_maximum_cardinality_bipartite_matching()

◆ compute_min_cut()

◆ copy_graph()

◆ depth_first_traversal()

◆ digraph_graphviz()

◆ edge_connectivity()

◆ find_breadth_first_spanning_tree()

◆ find_depth_first_spanning_tree()

◆ find_min_path() [1/3]

◆ find_min_path() [2/3]

◆ find_min_path() [3/3]

◆ find_path_breadth_first()

◆ find_path_depth_first()

◆ foldl_arcs() [1/2]

◆ foldl_arcs() [2/2]

◆ foldl_nodes()

◆ for_each_arc() [1/3]

◆ for_each_arc() [2/3]

◆ for_each_arc() [3/3]

◆ for_each_in_arc()

◆ for_each_node()

◆ for_each_out_arc()

◆ forall_arc() [1/2]

◆ forall_arc() [2/2]

◆ forall_node()

◆ generate_cross_graph()

◆ generate_graphpic()

◆ generate_graphviz() [1/2]

◆ generate_graphviz() [2/2]

◆ generate_net_graph()

◆ graph_to_tree_node()

◆ in_arcs()

◆ in_degree()

◆ in_nodes()

◆ in_pairs()

◆ inconnected_components()

◆ inter_copy_graph()