| |
|
|
| |
|
|
| |
|
|
| |
La relación para calcular el flujo en la tubería a partir de la medida de velocidad del lazo se puede obtener como sigue. |
|
| |
|
|
| |
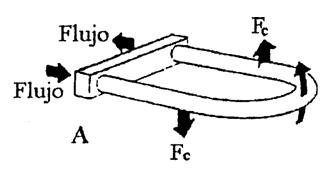
Cuando el fluido fluye en el lazo es forzado a tomar la velocidad vertical creciente (Vv) en el momento que entra al lazo y decreciente cuando sale del mismo, por lo cual aparece la aceleración de Coriolis. La velocidad (Vv) es perpendicular a la velocidad del fluido Vh. |
|
| |
|
|
| |
La aceleración de Coriolis esta dada por: |
|
| |
|
|
| |
donde: |
|
| |
ac= aceleración de Coriolis
Vh = velocidad del fluido a lo largo del tubo
ω = velocidad angular (movimiento del tubo) |
|
| |
|
|
| |
Por la segunda ley de Newton queda: |
|
| |
|
|
| |
Donde: |
|
| |
Fc = fuerza de Coriolis
m = masa de fluido |
|
| |
|
|
| |
Para determinar el flujo másico se requiere determinar el momento creado en el lazo por la fuerza de Coriolis actuando sobre el mismo, que son F1 y F2 actuando en direcciones opuestas sobre el lazo. |
|
| |
|
|
| |
El lazo vibra alrededor del eje O-O debido a la acción de la bobina electromagnética y las fuerzas de Coriolis crean un momento oscilatorio (M) alrededor del eje R-R. Este momento viene dado por: |
|
| |
|
|
| |
Como F1 = F2 = Fc y r1 = r2 = r entonces: M = 2Fr |
|
| |
|
|
| |
Combinando las expresiones anteriores se obtiene: |
|
| |
|
|
| |
La velocidad Vh se define como la longitud por unidad de tiempo: |
|
| |
|
|
| |
donde: |
|
| |
L = longitud del lazo.
Δt = tiempo en que tarda el lazo en pasar dos veces consecutivas por el punto neutro. |
|
| |
|
|
| |
La rata de flujo másico (Q) se define como la masa que pasa por un punto dado por unidad de tiempo |
|
| |
|
|
| |
Luego con las dos ecuaciones tenemos que |
|
| |
|
|
| |
Sustituyendo en la ecuación del momento obtenemos: |
|
| |
|
|
| |
El desplazamiento angular (θ) debido al momento (M) es contrarrestado por la rigidez del tubo sensor. |
|
| |
|
|
| |
En general, para cualquier resorte de torsión se cumple: |
|
| |
|
|
| |
Debido a que T = M, se obtiene: |
|
| |
|
|
| |
Las vibraciones introducidas al lazo por la bobina electromagnética y el momento generado como respuesta al efecto Coriolis originan desplazamientos como se muestra en la figura. |
|
| |
|
|
| |
 |
|
| |
|
|
| |
|
|
| |
La rata de flujo másico se puede inferir midiendo el desplazamiento angular (θ), para lo cual se deberán utilizar sensores en cada extremo del lazo. Esta medición se hace sensando el tiempo en el que cada sensor detecta el punto medio de su lado respectivo. |
|
| |
|
|
| |
La diferencia de tiempo a flujo cero es nula. A medida que el flujo se incrementa, la diferencia de tiempo entre las señales (Δt) también se incrementa. La velocidad del tubo en el punto medio de su recorrido (Vv) se relaciona con (θ) según la siguiente relación trigonométrica: |
|
| |
|
|
| |
Si (θ) es pequeño éste se aproxima a sin(θ). También, para pequeñas rotaciones Vv es el producto de ω por el largo del tubo (L), luego: |
|
| |
|
|
| |
Combinando las expresiones anteriores se obtiene: |
|
| |
|
|
| |
De esta última expresión se deduce que el flujo másico es directamente proporcional a las dimensiones físicas del medidor, a la rigidez del tubo y a Δt, y es independiente de la frecuencia de vibración. |
|
| |
|
|
| |
La medición de Δt provee una forma directa de medir el flujo másico. |
|
| |
|
|
| |
|
|
| |
 |
|
|
| |
|
|
