ula
 
temas
 
 
 
 
 
   
     
 
 
     
 
Si aplicamos la ecuación de Bernoulli entre un punto en la tubería (1) y un punto en la contracción (2) tendremos:
  
 

 
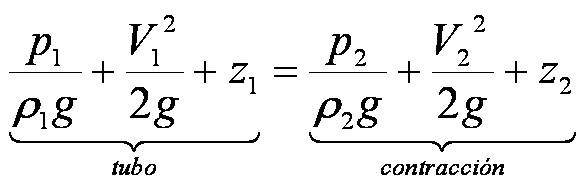
  Ecuación de la conservación de la masa (continuidad)  
 

 
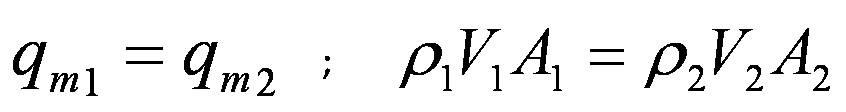
  Observaciones:  
 

  • Como la diferencia de cotas es pequeña así el instrumento se monte verticalmente

  • Si suponemos inicialmente que el flujo es incompresible

  
  La ecuación de Bernouilli queda:  
 
 
  Reordenando la ecuación convenientemente:  
 
 
 

De la ecuación de continuidad:

  
 
 
Donde:  
 
  Luego:  
 
 
     
 
 
     
 
 
     
 
 
     
  La ecuación básica para medición de flujo con reducción de área es:  
 
 
  Si queremos calcular el flujo másico tendremos que multiplicar la ecuación por la densidad obteniendo:  
  resolviendo:  
 
 
     
 
 
     

 
©