Si un plano (a) se encuentra en una posición cualquiera con respecto a un sistema de doble proyección ortogonal (H-V), Puede establecerse un nuevo sistema de doble proyección ortogonal (4-3), con respecto al cual el plano (a) sea un plano horizontal, por medio de dos cambios de plano de proyección sucesivos, realizados en la siguiente forma:

 

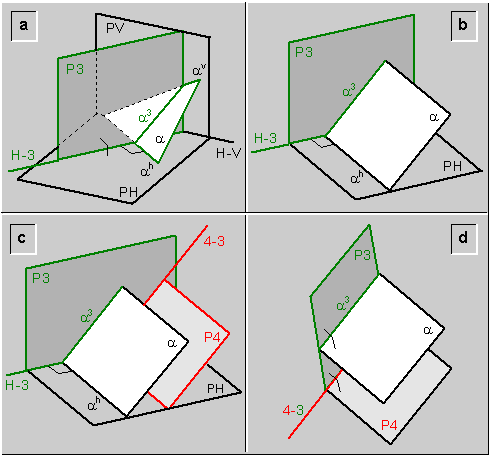
a)     Se cambia el plano vertical de proyección (PV) por un plano tres de proyección (P3), perpendicular a la traza horizontal del plano (a) (fig.6a). Se establece de esta forma el sistema de doble proyección ortogonal (H-3), en el cual, el plano (a) es un plano de punta\ fig.6b.

 

 

b)    Se cambia el plano horizontal de proyección (PH) por un plano cuatro de proyección (P4), paralelo al plano (a) (fig.6c). Se establece de esta forma el sistema de doble proyección ortogonal (4-3), en el cual, el plano (a) es un plano horizontal\ fig.6d.

 

 

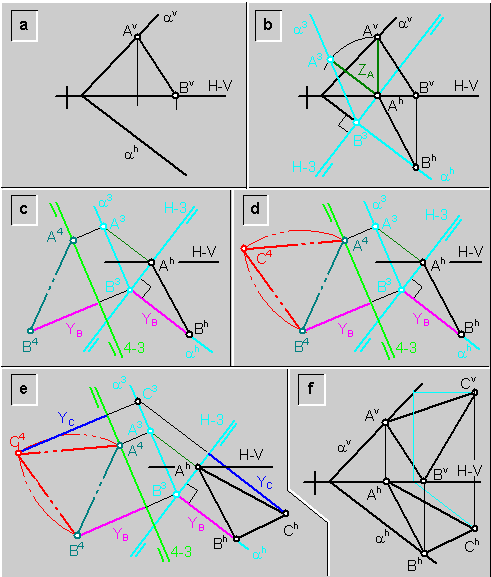
Ejemplo: Definir las proyecciones del triángulo equilátero de vértices (A;B;C), contenido en el plano (a), sabiendo que el vértice (C) esta a la derecha de (A)\ fig.7a.

 

Solución:

 

a)     Se define la proyección horizontal (A^h-B^h) del lado (A-B), haciéndolo pertenecer al plano (a)\ fig.7b.

Se establece, por medio de la nueva línea de tierra (H-3), el cambio del plano vertical de proyección (PV) por el plano tres de proyección (P3), el cual es perpendicular a la traza horizontal del plano (a). En este sistema de doble proyección ortogonal (H-3), el plano (a) se observa de punta.

Se define la proyección tres (a³) de la traza tres del plano (a); y las proyecciones (A³ y B³) de los puntos (A y B), por medio del traslado de sus respectivas cotas (Z_A y Z_B); la cota de (B) es cero (Z_B=0).

 

 

b)    Se establece, por medio de la nueva línea de tierra (4-3), el cambio del plano horizontal de proyección por un plano cuatro  (P4), paralelo al plano (a)\ fig.7c.

En este nuevo sistema de doble proyección ortogonal, el plano (a) es un plano horizontal, encontrándose su proyección sobre el plano cuatro en verdadero tamaño.

Se definen las proyecciones (A⁴ y B⁴) de los puntos (A y B), trasladando sus respectivos vuelos (Y_A y Y_B); el vuelo (Y_A) del punto (A) es cero (Y_A=0).

c)     Se dibuja, en verdadero tamaño, la proyección cuatro (A⁴;B⁴;C⁴) del triángulo equilátero (A;B;C)\ fig.7d.

d)    Se define la proyección tres (A³;B³;C³) del triángulo (A;B;C)\ fig.7e.

Se define la proyección horizontal (A^h;B^h;C^h) del triángulo (A;B;C); trasladando el vuelo (Y_C) del punto (C).

e)    Se define la proyección vertical (A^v;B^v;C^v) del triángulo (A;B;C); haciendo pertenecer el punto (C) al plano (a) \ fig.7f.

---