#include <tpl_binTreeOps.H>
|
|
using | Key = typename Node::key_type |
| |
|
using | key_type = typename Node::key_type |
| | The type of key.
|
| |
|
|
Cmp & | key_comp () noexcept |
| | Return the comarison criteria.
|
| |
| Cmp & | get_compare () noexcept |
| |
| | BinTree_Operation (Cmp __cmp=Cmp()) noexcept |
| | The type of key. More...
|
| |
| Node * | search (Node *root, const Key &key) noexcept |
| |
| Node * | search_parent (Node *root, const Key &key, Node *&parent) noexcept |
| |
| Node * | search_rank_parent (Node *root, const Key &key) noexcept |
| |
| Node * | insert (Node *&root, Node *p) noexcept |
| |
| Node * | insert_dup (Node *&root, Node *p) noexcept |
| |
| Node * | search_or_insert (Node *&r, Node *p) noexcept |
| |
| bool | split_key_rec (Node *&root, const Key &key, Node *&ts, Node *&tg) noexcept |
| |
| void | split_key_dup_rec (Node *root, const typename Node::key_type &key, Node *&ts, Node *&tg) noexcept |
| |
| Node * | remove (Node *&root, const Key &key) noexcept |
| |
| Node * | insert_root (Node *&root, Node *p) noexcept |
| |
| Node * | insert_dup_root (Node *&root, Node *p) noexcept |
| |
| Node * | join_preorder (Node *t1, Node *t2, Node *&dup) noexcept |
| |
| Node * | join (Node *t1, Node *t2, Node *&dup) noexcept |
| |
| void | split_key (Node *root, const Key &key, Node *&l, Node *&r) noexcept |
| |
| Node * | insert_root_rec (Node *root, Node *p) noexcept |
| |
| Node * | search_or_insert_root_rec (Node *root, Node *p) noexcept |
| |
template<class Node, class Cmp = Aleph::less<typename Node::key_type>>
class Aleph::BinTree_Operation< Node, Cmp >
Functor encompassing basic operation for binary search trees.
- See also
- BinNode
◆ BinTree_Operation()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
The type of key.
Initialize the functor with comarison criteria __cmp
◆ get_compare()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.
◆ insert()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Insert a node p in a binary search tree
insert(root, p) inserts the node p in the binary search tree with root
- Parameters
-
| [in,out] | root | of tree |
| [in] | p | pointer to the node to be inserted |
- Returns
p if this was inserted; that is if p->get_key() is not in the tree; otherwise, Node::NullPtr is returned
◆ insert_dup()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Insert a node p in a binary search tree
insert_dup(root, p) inserts the node p in the binary search tree with root. The key contained in p can be already present in the tree.
- Parameters
-
| [in,out] | root | of tree |
| [in] | p | pointer to the node to be inserted |
- Returns
- the pointer
p
◆ insert_dup_root()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Insert node p as root of a binary search tree. The key of p can be duplicated.
- Parameters
-
| [in,out] | root | of tree |
| [in] | p | node to insert as root |
- Returns
- the pointer
p which has became the root of tree
◆ insert_root()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Insert the node p as root of a binary search tree
insert_root(root, p) inserts in the tree root the node p. After insertion, p becomes the new root of tree.
- Parameters
-
| [in,out] | root | of binary search tree |
| [in] | p | pointer to node to insert |
- Returns
- a pointer to
p if this was inserted; that is, if p->get_key() was not present in the tree. Otherwise, no insertion is done and Node::NullPtr is returned
◆ insert_root_rec()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Insert a node as root in a binary search tree.
This version first insert p as a leaf of tree. Then p is rotated until the root.
- Parameters
-
| [in] | root | of tree |
| [in] | p | pointer to the node to insert |
- Returns
- pointer to
p if p->get_key() is not in the tree. Otherwise the function returns Node::NullPtr
◆ join()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Fast union of two binary search trees
join(t1, t2, dup) joins the nodes of t1 with the nodes of t2. The duplicated keys of t2 are copied in the binary search tree dup.
- Parameters
-
| [in] | t1 | root of first tree |
| [in] | t2 | root of second tree |
| [out] | dup | tree where the duplicated keys of t2 are put |
- Returns
- pointer to the root of resulting join
◆ join_preorder()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Union of two binary search trees
- Warning
- This union is
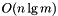 where n and m are the sizes of
where n and m are the sizes of t1 and t2respectively. Use join() which is much more faster
- Parameters
-
| [in] | t1 | root of first tree |
| [in] | t2 | root of second tree |
| [out] | dup | root of tree where the duplicated keys will be put |
- Returns
- a pointer to the resulting root of tree
◆ remove()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Remove a key from a binary search tree
- Parameters
-
| [in,out] | root | of tree |
| [in] | key | to remove |
- Returns
- a valid pointer to the removed node if
key was found in the tree, Node::NullPtr otherwise
◆ search()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Search a node with a specific key.
- Parameters
-
| [in] | root | of the tree |
| [in] | key | to be searched |
- Returns
- a pointer to a node containing the key if this was found;
Node::NullPtr otherwise
◆ search_or_insert()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Search or insert a node in a binary search tree.
search_or_insert(root, p) searches in root a node containing p->get_key(). If found, then this node is returned. Otherwise p is inserted and returned.
- Parameters
-
| [in,out] | r | roor of tree |
| [in] | p | node to search or insert |
- Returns
p if its key was not in the tree; otherwise, a pointer containing the tree is returned.
◆ search_or_insert_root_rec()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Search and eventually insert p as root in a binary search tree
- Parameters
-
| [in] | root | of tree |
| [in] | p | pointer to the node to eventually insert |
- Returns
- if
p is inserted, then it returns p; otherwise, it returns a pointer to the tree node containing to p->get_key()
◆ search_parent()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Search a key and find its node and parent.
- Parameters
-
| [in] | root | of tree |
| [in] | key | to search |
| [out] | parent | pointer to parent node if key was found. Otherwise value is indetermined |
- Returns
- a valid pointer to a node containing
key if this is found; otherwise, it returns a pointer to the last visited node
◆ split_key()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Split a binary search tree according to a key.
split_key(root, key, l, r) splits the tree root according to key. At the end, l contains all the keays lesser than key and r all the keys greater or equal than key.
- Parameters
-
| [in,out] | root | of tree to split |
| [in] | key | for splitting |
| [out] | l | tree with keys lesser than key |
| [out] | r | tree with keys greater or equal than key |
◆ split_key_dup_rec()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
| void Aleph::BinTree_Operation< Node, Cmp >::split_key_dup_rec |
( |
Node * |
root, |
|
|
const typename Node::key_type & |
key, |
|
|
Node *& |
ts, |
|
|
Node *& |
tg |
|
) |
| |
|
inlinenoexcept |
Split a tree according to a key value
split_key_dup_rec(root, key, ts, tg) splits according to key the tree withrootand build two trees.t1contains the keys lesser thankeyandt2the keys greater or equal thankey`.
- Parameters
-
| [in,out] | root | of tre to be split |
| [in] | key | for splitting |
| [out] | ts | tree with the keys lesser than key |
| [out] | tg | tree with the keys greater or equal than key |
◆ split_key_rec()
template<class Node , class Cmp = Aleph::less<typename Node::key_type>>
Split recursively according to a key.
split_key_rec(root, key, ts, tg) splits the tree with root in two trees t1 which contain the keys lesser than key and t2 which contains the keys greater than key.
The split only is performed if key is not in the tree.
- Parameters
-
| [in,out] | root | of tree |
| [in] | key | for slitting |
| [out] | ts | tree with keys lesser than key |
| [out] | tg | tree with keys greater than key |
- Returns
true if the tree wa split; that if key was not in the tree. Otherwise the split is not performed and it return false
The documentation for this class was generated from the following file:
 Inheritance diagram for Aleph::BinTree_Operation< Node, Cmp >:
Inheritance diagram for Aleph::BinTree_Operation< Node, Cmp >: Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: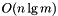 where n and m are the sizes of
where n and m are the sizes of  Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: