Macros | |
| #define | DECLARE_BINNODE(Name, height, Control_Data) |
| #define | DECLARE_BINNODE_SENTINEL(Name, height, Control_Data) |
Functions | |
| template<typename Node , class Write = Dft_Write<Node>> | |
| void | Aleph::generate_tree (Node *root, std::ostream &out, const int &tree_number=0) |
| template<typename Node , class Write = Dft_Write<Node>> | |
| void | Aleph::generate_forest (Node *root, std::ostream &out) |
| template<typename Node , class Write > | |
| void | Aleph::generate_btree (Node *root, std::ostream &out) |
| void | huffman_to_btreepic (Freq_Node *p, const bool with_level_adjust=false) |
| template<class Node , typename Key > | |
| Node * | Aleph::build_optimal_tree (Key keys[], double p[], const size_t n) |
| template<class Node > | |
| Node * | Aleph::select_gotoup_root (Node *root, const size_t &i) |
| template<class Node > | |
| Node *& | Aleph::LLINK (Node *p) noexcept |
| template<class Node > | |
| Node *& | Aleph::RLINK (Node *p) noexcept |
| template<class Node > | |
| Node::Key_Type & | Aleph::KEY (Node *p) noexcept |
| template<class Node > | |
| int | Aleph::inOrderRec (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node > | |
| int | Aleph::preOrderRec (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node > | |
| int | Aleph::postOrderRec (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node , class Op > | |
| void | Aleph::for_each_in_order (Node *root, Op &&op) noexcept(noexcept(op)) |
| template<class Node , class Op > | |
| void | Aleph::for_each_preorder (Node *root, Op &&op) |
| template<class Node , class Op > | |
| void | Aleph::for_each_postorder (Node *root, Op &&op) |
| template<class Node > | |
| DynList< Node * > | Aleph::prefix (Node *root) |
| template<class Node > | |
| DynList< Node * > | Aleph::infix (Node *root) |
| template<class Node > | |
| DynList< Node * > | Aleph::suffix (Node *root) |
| template<class Node > | |
| size_t | Aleph::compute_cardinality_rec (Node *root) noexcept |
| template<class Node > | |
| size_t | Aleph::computeHeightRec (Node *root) noexcept |
| template<class Node > | |
| void | Aleph::destroyRec (Node *&root) noexcept |
| template<class Node > | |
| Node * | Aleph::copyRec (Node *root) |
| template<class Node > | |
| void | Aleph::levelOrder (Node *root, void(*visitFct)(Node *, int, bool)) |
| template<class Node , class Operation > | |
| bool | Aleph::level_traverse (Node *root, Operation &operation) |
| template<template< class > class Node, typename Key > | |
| Node< Key > * | Aleph::build_tree (const DynArray< Key > &preorder, long l_p, long r_p, const DynArray< Key > &inorder, long l_i, long r_i) |
| template<class Node > | |
| DynDlist< Node * > | Aleph::compute_nodes_in_level (Node *root, const int &level) |
| template<class Node > | |
| void | Aleph::inOrderThreaded (Node *root, void(*visitFct)(Node *)) |
| template<class Node > | |
| void | Aleph::preOrderThreaded (Node *node, void(*visitFct)(Node *)) |
| template<class Node > | |
| size_t | Aleph::internal_path_length (Node *p) noexcept |
| template<class Node > | |
| void | Aleph::tree_to_bits (Node *root, BitArray &array) |
| template<class Node > | |
| BitArray | Aleph::tree_to_bits (Node *root) |
| template<class Node > | |
| Node * | Aleph::bits_to_tree (const BitArray &array, int idx=0) |
| template<class Node > | |
| void | Aleph::save_tree_keys_in_prefix (Node *root, ostream &output) |
| template<class Node > | |
| void | Aleph::load_tree_keys_in_prefix (Node *root, istream &input) |
| template<class Node > | |
| void | Aleph::save_tree (Node *root, ostream &output) |
| template<class Node > | |
| Node * | Aleph::load_tree (istream &input) |
| template<class Node , class Get_Key > | |
| void | Aleph::save_tree_in_array_of_chars (Node *root, const string &array_name, ostream &output) |
| template<class Node , class Load_Key > | |
| Node * | Aleph::load_tree_from_array (const unsigned char bits[], const size_t &num_bits, const char *keys[]) |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| bool | Aleph::check_bst (Node *p, Compare cmp=Compare()) |
| template<class Node > | |
| Node * | Aleph::preorder_to_bst (DynArray< typename Node::key_type > &preorder, int l, int r) |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::searchInBinTree (Node *root, const typename Node::key_type &key, Compare cmp=Compare()) noexcept |
| template<class Node > | |
| Node * | Aleph::find_min (Node *root) noexcept |
| template<class Node > | |
| Node * | Aleph::find_max (Node *root) noexcept |
| template<class Node > | |
| Node * | Aleph::find_successor (Node *p, Node *&pp) noexcept |
| template<class Node > | |
| Node * | Aleph::find_predecessor (Node *p, Node *&pp) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::search_parent (Node *root, const typename Node::key_type &key, Node *&parent, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::search_rank_parent (Node *root, const typename Node::key_type &key, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::insert_in_bst (Node *&r, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::insert_dup_in_bst (Node *&root, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::search_or_insert_in_bst (Node *&r, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| bool | Aleph::split_key_rec (Node *&root, const typename Node::key_type &key, Node *&ts, Node *&tg, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| void | Aleph::split_key_dup_rec (Node *&root, const typename Node::key_type &key, Node *&ts, Node *&tg, Compare cmp=Compare()) noexcept |
| template<class Node > | |
| Node * | Aleph::join_exclusive (Node *&ts, Node *&tg) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::remove_from_bst (Node *&root, const typename Node::key_type &key, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::insert_root (Node *&root, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::insert_dup_root (Node *&root, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::join_preorder (Node *t1, Node *t2, Node *&dup, Compare cmp=Compare()) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::join (Node *t1, Node *t2, Node *&dup, Compare cmp=Compare()) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_right (Node *p) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_right (Node *p, Node *pp) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_left (Node *p) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_left (Node *p, Node *pp) noexcept |
| template<class Node , class Key , class Compare = Aleph::less<typename Node::key_type>> | |
| void | Aleph::split_key (Node *&root, const Key &key, Node *&l, Node *&r, Compare cmp=Compare()) noexcept |
| template<class Node > | |
| void | Aleph::swap_node_with_successor (Node *p, Node *&pp, Node *q, Node *&pq) noexcept |
| template<class Node > | |
| void | Aleph::swap_node_with_predecessor (Node *p, Node *&pp, Node *q, Node *&pq) noexcept |
| template<class Node , class Key , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::insert_root_rec (Node *root, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Key , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::search_or_insert_root_rec (Node *root, Node *p, Compare cmp=Compare()) noexcept |
| template<class Node , class Op > | |
| bool | Aleph::prefix_traverse (Node *root, Op op) noexcept(noexcept(op)) |
| template<class Node , class Op > | |
| bool | Aleph::infix_traverse (Node *root, Op op) noexcept(noexcept(op)) |
| template<class Node > | |
| auto & | Aleph::COUNT (Node *p) noexcept |
| template<class Node > | |
| Node * | Aleph::select_rec (Node *r, const size_t i) |
| template<class Node > | |
| Node * | Aleph::select_ne (Node *r, const size_t pos) noexcept |
| template<class Node > | |
| Node * | Aleph::select (Node *r, const size_t pos) |
| template<class Node > | |
| Node * | Aleph::select (Node *root, const size_t pos, Node *&parent) |
| template<class Node , class Compare > | |
| long | Aleph::inorder_position (Node *r, const typename Node::key_type &key, Node *&p, Compare &cmp) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| long | Aleph::find_position (Node *r, const typename Node::key_type &key, Node *&p, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| Node * | Aleph::insert_by_key_xt (Node *&r, Node *p, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| Node * | Aleph::insert_dup_by_key_xt (Node *&r, Node *p, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| bool | Aleph::split_key_rec_xt (Node *&root, const typename Node::key_type &key, Node *&l, Node *&r, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| void | Aleph::split_key_dup_rec_xt (Node *&root, const typename Node::key_type &key, Node *&l, Node *&r, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| Node * | Aleph::insert_root_xt (Node *&root, Node *p, Compare &cmp) noexcept |
| template<class Node , class Compare > | |
| Node * | Aleph::insert_dup_root_xt (Node *&root, Node *p, Compare &cmp) noexcept |
| template<class Node > | |
| void | Aleph::split_pos_rec (Node *&r, const size_t i, Node *&ts, Node *&tg) |
| template<class Node > | |
| void | Aleph::insert_by_pos_xt (Node *&r, Node *p, size_t pos) |
| template<class Node > | |
| Node * | Aleph::join_exclusive_xt (Node *&ts, Node *&tg) noexcept |
| template<class Node , class Compare = Aleph::less<typename Node::key_type>> | |
| Node * | Aleph::remove_by_key_xt (Node *&root, const typename Node::key_type &key, Compare &cmp) noexcept |
| template<class Node > | |
| Node * | Aleph::remove_by_pos_xt (Node *&root, size_t pos) |
| template<class Node > | |
| bool | Aleph::check_rank_tree (Node *root) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_right_xt (Node *p) noexcept |
| template<class Node > | |
| Node * | Aleph::rotate_to_left_xt (Node *p) noexcept |
| Node * | Aleph::BinTree_Operation< Node, Cmp >::search_rank_parent (Node *root, const Key &key) noexcept |
| long | Aleph::BinTreeXt_Operation< Node, Cmp >::inorder_position (Node *r, const Key &key, Node *&p) noexcept |
| Node * | Aleph::BinTreeXt_Operation< Node, Cmp >::insert_root (Node *&root, Node *p) noexcept |
| DynSetTree & | Aleph::DynSetTree< Key, Tree, Compare >::join (DynSetTree &t, DynSetTree &dup) |
| DynSetTree & | Aleph::DynSetTree< Key, Tree, Compare >::join_dup (DynSetTree &t) |
| std::pair< long, Node * > | Aleph::Gen_Rand_Tree< NodeType, Key, Compare >::position (const Key &key) noexcept |
| std::pair< int, Node * > | Aleph::Gen_Treap_Rk< NodeType, Key, Compare >::position (const Key &key) const noexcept |
| template<class Node > | |
| void | Aleph::tree_preorder_traversal (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node > | |
| void | Aleph::forest_preorder_traversal (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node > | |
| void | Aleph::tree_postorder_traversal (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node > | |
| void | Aleph::forest_postorder_traversal (Node *root, void(*visitFct)(Node *, int, int)) |
| template<class Node , class Eq > | |
| bool | Aleph::are_tree_equal (Node *t1, Node *t2, Eq &eq) noexcept(noexcept(eq(t1->get_key(), t2->get_key()))) |
| template<class Node > | |
| void | Aleph::destroy_tree (Node *root) |
| template<class Node > | |
| void | Aleph::destroy_forest (Node *root) |
| template<class Node > | |
| size_t | Aleph::compute_height (Node *root) |
| template<class Node > | |
| Node * | Aleph::deway_search (Node *root, int path [], const size_t &size) |
| template<class Node , class Equal = Aleph::equal_to<typename Node::key_type>> | |
| Node * | Aleph::search_deway (Node *root, const typename Node::key_type &key, int deway [], const size_t &size, size_t &n) |
| template<class TNode , class BNode > | |
| BNode * | Aleph::forest_to_bin (TNode *root) |
| template<class TNode , class BNode > | |
| TNode * | Aleph::bin_to_forest (BNode *broot) |
| template<class Node > | |
| unsigned long & | Aleph::PRIO (Node *p) noexcept |
Aleph-w (  ) mamages several types of trees.
) mamages several types of trees.
General rooted trees and forests can be specified through the class Tree_Node<T>, which defines nodes containing a generic key of type T.
Tree_Node<T> is relativelly simple but very powerful and useful for modeling problems based in general trees and resident in the memory.
Aleph-w (  ) support an extense variety of binary search tre types designed for managing operation on sets in
) support an extense variety of binary search tre types designed for managing operation on sets in  complexity.
complexity.
The main types are Avl_Tree, Splay_Tree, Rand_Tree, Treap, Treap_Rk, Rb_Tree and others.
These classes operate in function of "nodes" not of the data contained in the nodes, which allows a more powerful and functional interface, although certainly more complicated for using because the memory management is delegated to the user.
Managing of sets and maps based on the binary search trees metioned above could be implemented with memory management through of two general classes
DynSetTree: implement setsDynMapTree: implement mapsFor both classes you could specify the binary search tree type as template parameter and decide its performance characteristics.
Heaps are indispensable for the good performance of many algorithms. Aleph-w (  ) supports several types of heaps, whose usage is according the algorithms needs.
) supports several types of heaps, whose usage is according the algorithms needs.
BinHeap: a binary heap oriented to nodes containing data. The heap type is ideal for application managing dynamic data that can belong to several heaps. The great advantage of this type is its scalability.DynBinHeap: a version of above heap where the memory management is already done.ArrayHeap: a heap based on a contiguous array representation. This is the fastest heap, but once decided the array size, the scale is limited.DynArrayHeap: similar to above but uses DynArray, what gives a good trade of between performance and memory consumption.In Aleph-w (  ) the binary trees are managed by nodes, not by the keys that these contain. Many tree operations, concretlly those modifiying them, take as parameters nodes. For example, ig you have a binary search
) the binary trees are managed by nodes, not by the keys that these contain. Many tree operations, concretlly those modifiying them, take as parameters nodes. For example, ig you have a binary search tree of intergers and you want to insert 10, then you must first allocate the node, put it the key and then insert into the tree. Some such as:
Bintree<int>::Node * p = new Bintree<int>::Node(10); tree.insert(p);
This usage is some complicated and tedious most of the time. However, it simplifies enormously the tree algorithms, since these do not neet to worry by memory management. Eventually, it could also simplificate the user's life and definitively improve the performance. Suppose for example that you have two trees and you need to remove a key from one and insert it into the another. In this case you could do as follows:
auto ptr = tree.remove(10); // remove node with 10 and return ptr tree2.insert(ptr);
If the tree managed the memory, then the removal from tree1 would perform a delete. Afterward, in order to insert 10 into tree2 it would be need to allocate the node, copy it the 10 and insert it into the tree. As you see
If this sound some complicated, do not worry. Aleph-w ( 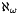 ) exports other interfaces that wrappes and automatize the memory management.
) exports other interfaces that wrappes and automatize the memory management.
Another advantage of Aleph-w ( 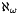 ) approach for binary trees is that it allows to extend the data contained in the nodes by inheritance. Suppose that you search by a integer value, but that you have several types of data. Consider for example
) approach for binary trees is that it allows to extend the data contained in the nodes by inheritance. Suppose that you search by a integer value, but that you have several types of data. Consider for example Student and Professor classes, then you could do:
Professor_Node : public BinTree<int>::Node { ... };
Student_Node : public BinTree<int>::Node { ... };
Since that tree operations are by BinTree<int>::Node, you could then insert student and professors nodes, and eventually other derived types, without need of change your insertion code. Of course, specific code related to a specific class will need to cast from BinTree<int>::Node to the correspondent derived class for some operations.
If you use the technique explained above and the derivated class is enough complex, then perhaps you need to call to the destructor of derived class when you perform delete on a node pointer. In this case, you need that the destructor of BinTree<int>::Node is virtual. In this situation you must use BinTreeVtl<int> in order to indicate that the node destructor is virtual.
The same approach is used for the remainder of binary trees: Avl, Splay, ...
This separation is desirable because if you know that do not need to call to the derived destructor, the you can save memory by using nodes with simple destructors.
| #define DECLARE_BINNODE | ( | Name, | |
| height, | |||
| Control_Data | |||
| ) |
Specify tree node for a binary tree.
DECLARE_BINNODE(Name, height, Control_Data) generates two classes of binary nodes called Name and NameVtl, respectevely. The only difference is expressed by the fact that for NameVtl its destructor is virtual.
Each node has an attribute called key, accessible through KEY(p) or p->get_key(), where p is a pointer to the node.
A binary node has two static attributes:
NullPtr which represents to the empty treeMaxHeight: an estimated value of maximun height of tree. This value is used as helper for recursive and stack based algorithms for allocate enough stack space.| Name | the name of class defining the node. |
| height | maximun height that could have the tree |
| Control_Data | control data according to tree type |
| #define DECLARE_BINNODE_SENTINEL | ( | Name, | |
| height, | |||
| Control_Data | |||
| ) |
Specify tree node for a binary tree.
DECLARE_BINNODE_SENTINEL(Name, height, Control_Data) generates two classes of binary nodes called Name and NameVtl, respectevely. The only difference is expressed by the fact that for NameVtl its destructor is virtual.
In this version, a special static member called sentinel_node is declared. In this context, a sentinel node is a node representing the empty tree whose state is initialized by the call to Control_Data(sentinelCtor).
Each node has an attribute called key, accessible through KEY(p) or p->get_key(), where p is a pointer to the node.
A binary node has two static attributes:
NullPtr which represents to the empty treeMaxHeight: an estimated value of maximun height of tree. This value is used as helper for recursive and stack based algorithms for allocate enough stack space.| Name | the name of class defining the node. |
| height | maximun height that could have the tree |
| Control_Data | control data according to tree type |
|
inlinenoexcept |
Retorna true si t1 es igual a t2
|
inline |
Convierte un árbol binario a su arborescencia equivalente.
bin_to_forest(root) toma un árbol binario derivado de BinNode y lo convierte a su arborescencia equivalente.
La rutina maneja dos parámetros tipo:
El procedimiento asume que ambos tipos comparten el mismo tipo de clave.
| [in] | broot | raÃz del árbol binario a convertir. |
| bad_alloc | si no hay suficiente memoria. |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Build a binary tree given its bits code.
bits_to_tree(array, idx) takes a bit array array and from the starting index idx builds the corresponding tree.
| [in] | array | bits array |
| [in] | idx | starting index |
| bad_alloc | if there is no enough memory |
| Node* Aleph::build_optimal_tree | ( | Key | keys[], |
| double | p[], | ||
| const size_t | n | ||
| ) |
Construye un árbol binario de búsqueda óptimo según frecuencias estimadas de búsqueda.
build_optimal_tree(keys,p,n) construye un árbol binario de búsqueda óptimo que contiene n claves almacenadas en el arreglo keys[], cada clave con frecuencia o probabilidad de búsqueda almacenada en el arreglo p[], paralelo a keys[].
| [in] | keys | arreglo contentivo de las claves. |
| [in] | p | arreglos contentivo de las probabilidades de aparición o búsqueda. |
| [in] | n | cantidad total de claves; esta es la dimensión de los arreglos. |
| bad_alloc | si no hay suficiente memoria. |
|
inline |
Build a binary tree form its preorder and inorder traversals
build_tree() takes two dynamic arrays with the preorder and inorder traversal of keys and builds the correspondent tree.
| [in] | preorder | array with the preorder traversal |
| [in] | l_p | first index in preorder |
| [in] | r_p | last index in preorder |
| [in] | inorder | array with the preorder traversal |
| [in] | l_i | first index in inorder |
| [in] | r_i | last index in inorder |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Return true if p is a binary search tree
| [in] | p | root of the tree |
| [in] | cmp | comparison criteria |
true if p is a binary search tree according to Compare criteria.  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Return true if root is a valid extended binary tree.
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Count the number of nodes of a binary tree
| [in] | root | of tree |
 Here is the call graph for this function:
Here is the call graph for this function:| size_t Aleph::compute_height | ( | Node * | root | ) |
Calcula la altura del árbol root.
| [in] | root | raÃz del árbol. |
|
inline |
Count the number of nodes in a specific tree level
| [in] | root | of tre |
| [in] | level | desired to be counted |
level | bad_alloc | if there is no enough memory |
|
inlinenoexcept |
Compute recursively the height of root
| [in] | root | of tree |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Copy recursively a tree
| [in] | root | of tre to be copied |
root | bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Return the number of nodes of the tree fron p is root.
| p | pointer to root |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Destruye (libera memoria) la arborescencia cuya primer árbol es root.
destroy_forest(root) libera toda la memoria ocupada por el la arborescencia cuyo primer árbol tiene raÃz root.
| [in] | root | raÃz del primer árbol de la arborescencia que se desea destruir. |
| domain_error | si root no es nodo raÃz del árbol más a la izquierda de la arborescencia. |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Destruye (libera memoria) el árbol cuya raÃz es root.
destroy_tree(root) libera toda la memoria ocupada por el árbol cuya raÃz es root.
| [in] | root | raÃz del árbol que se desea liberar. |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Free recursively all the memory occuped by the tree root
new operator.| [in] | root | of tree to free |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Retorna un nodo de una arborescencia dado su número de Deway.
deway_search(root,path,size) toma el número de Deway guardado en path, de longitud size y busca en la arborescencia cuyo primer árbol es root un nodo que se corresponda con el número de Deway dado.
| [in] | root | raÃz del primer árbol de la arborescencia. |
| [in] | path | arreglo que contiene el número de Deway. |
| [in] | size | tamaño del número de deway. |
|
inlinenoexcept |
Return the maximum key contained in a binary search tree
| [in] | root | of tree |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Return the minimum key contained in a binary search tree
| [in] | root | of tree |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Find the inorder position of a key in an extended binary search tree.
find_position(r, key, p, cmp) searches key in the tree with root r. If key is found then its inorder position is returned and a pointer to the node containing the key is written in output parameter p. Otherwise, the function returns the position that would have key if this was in the tree. At this regard, there are three cases:
key is lesser than the minimum key of tree, then -1 is returned and p is the node with the smallest key.key is greater than the maximum key in the tree, then the number of keys is returned and p is the node with the maximum key in the tree.key if this was in the tree and p is the node whose key is inmediataly greater than key.| [in] | r | root of tree |
| [in] | key | to be searched |
| [out] | p | reference to pointer to node |
| [in] | cmp | comparison criteria |
key in the tree  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Find the inorder predecessor of p
| [in] | p | a node pointer |
| [out] | pp | p's parent |
p  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Find the inorder successor of p
| [in] | p | a node pointer |
| [out] | pp | p's parent |
p  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Execute an operation in order sense for each node of tree.
| [in] | root | of tree |
| [in] | op | operation to be executed on each node |
| void Aleph::for_each_postorder | ( | Node * | root, |
| Op && | op | ||
| ) |
Execute an operation in postorder sense for each node of tree.
| [in] | root | of tree |
| [in] | op | operation to be executed on each node |
 Here is the call graph for this function:
Here is the call graph for this function:| void Aleph::for_each_preorder | ( | Node * | root, |
| Op && | op | ||
| ) |
Execute an operation in preorder sense for each node of tree.
| [in] | root | of tree |
| [in] | op | operation to be executed on each node |
|
inline |
Recorre en sufijo una arborescencia.
forest_postorder_traversal((root,visit) realiza un recorrido sufijo sobre el árbol con raÃz root. Si visitFct es especificado, entonces, por cada nodo visitado, se invoca la función.
La función de vista tiene la siguiente especificación:
void (visitFct)(Node p, int level, int pos)
Donde:
| [in] | root | raÃz del árbol a visitar. |
| [in] | visitFct | puntero a la función de visita. |
| domain_error | si root no es nodo raÃz del árbol más a la izquierda de la arborescencia. |
|
inline |
Recorre en prefijo una arborescencia.
forest_preorder_traversal((root,visit) realiza un recorrido prefijo sobre la arborescencia root. Si visitFct es especificado, entonces, por cada nodo visitado, se invoca la función.
La función de vista tiene la siguiente especificación:
void (visitFct)(Node p, int level, int pos)
Donde:
| [in] | root | raÃz del árbol primer árbol en la arborescencia. |
| [in] | visitFct | puntero a la función de visita. |
| domain_error | si root no es un nodo raÃz de un árbol. |
| BNode* Aleph::forest_to_bin | ( | TNode * | root | ) |
Convierte una arborescencia a su árbol binario equivalente.
forest_to_bin(root) toma una arborescencia derivada de Tree_Node y lo convierte a su equivalente árbol binario.
La rutina maneja dos parámetros tipo:
El procedimiento asume que ambos tipos comparten el mismo tipo de clave.
| [in] | root | raÃz del primer árbol perteneciente a la arborescencia a convertir. |
| bad_alloc | si no hay suficiente memoria. |
 Here is the call graph for this function:
Here is the call graph for this function:| void Aleph::generate_btree | ( | Node * | root, |
| std::ostream & | out | ||
| ) |
Genera una entrada para el programa de dibujado de árboles binarios btrepic.
Para escribir el contenido del nodo, la rutina usa la clase parametrizada Write, cuyo operador Write()(nodo) transforma la clave contenida en el nodo a la cadena que se desea sea escrita como contenido del nodo.
| [in] | root | raÃz del árbol a dibujar. |
| [out] | out | archivo asociado donde se desea escribir la especificación de dibujado. |
| void Aleph::generate_forest | ( | Node * | root, |
| std::ostream & | out | ||
| ) |
Genera una entrada para el programa de dibujado de árboles ntreepic.
generate_forest(root, out, tree_number) genera una especificación de dibujado de la arborescencia cuyo primer árbol es root para el programa de dibujado ntreepic. La salida es escrita en el archivo asociado a out.
Para escribir el contenido del nodo, la rutina usa la clase parametrizada Write, cuyo operador Write()(nodo) transforma la clave contenida en el nodo a la cadena que se desea sea escrita como contenido del nodo.
| [in] | root | raÃz del árbol a dibujar. |
| [out] | out | archivo asociado donde se desea escribir la especificación de dibujado. |
| void Aleph::generate_tree | ( | Node * | root, |
| std::ostream & | out, | ||
| const int & | tree_number = 0 |
||
| ) |
Genera una entrada para el programa de dibujado de árboles ntrepic.
generate_tree(root, out, tree_number) genera una especificación de dibujado del árbol con raÃz root para el programa de dibujado ntreepic. La salida es escrita en el archivo asociado a out.
Para escribir el contenido del nodo, la rutina usa la clase parametrizada Write, cuyo operador Write()(nodo) transforma la clave contenida en el nodo a la cadena que se desea sea escrita como contenido del nodo.
| [in] | root | raÃz del árbol a dibujar. |
| [out] | out | archivo asociado donde se desea escribir la especificación de dibujado. |
| [in] | tree_number | para uso interno NO USAR. |
| void huffman_to_btreepic | ( | Freq_Node * | p, |
| const bool | with_level_adjust = false |
||
| ) |
Genera una especificación para btreepic de un árbol de Huffman.
 Here is the call graph for this function:
Here is the call graph for this function:| DynList<Node*> Aleph::infix | ( | Node * | root | ) |
Return a list with inorder traversal of a tree
| [in] | root | of tree |
| bad_alloc | if there is no enough memory |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
noexcept |
Traverse a tree in preorder via its iterator and performs a conditioned operation on each item.
prefix_traverse(root, operation) instantiates the internal iterator of the class and traverses each item performing operation(p), where p is a node pointer.
operation must have the following signature:
bool operation(Node * p)
If operation(p) returns true then the iterator is advanced and the next item processed. Otherwise. the traversal stops.
| [in] | operation | to be performed on each item |
true if all the nodes were visited (operation on each one always returned true) or false if the traversal was stopped because there was a false result on an item. | anything | that could throw operation |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Compute the inorder position of a key
| [in] | r | root of tree |
| [in] | key | to be searched |
| [out] | p | pointer to the node containing key |
| [in] | cmp | comparison criteria |
key  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Compute the inorder position of a key
| [in] | r | root of tree |
| [in] | key | to be searched |
| [out] | p | pointer to the node containing key |
key if this is in the tree or -1 if key is not found  Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Traverse recursively inorder a binary tree.
inOrderRec(root,visit) performs a inorder traversal of tree rooted by root and on each node exceutes a visit function with the following signature:
void (*visitFct)(Node* p, int level, int pos)
Where:
p: pointer to visted node.level: level of node p.pos: ordinal indicating the visitt orderFor_Each_In_Order or traverse() instead| [in] | root | pointer to tree's root |
| [in] | visitFct | pointer to visit function |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Traverse inorder a binary tree without recursion and without stack.
inOrderThreaded(root,visit) traverses inorder the binary tree by building partial threads to succesor nodes. This implicates that during the traversal the links coulld be invalid.
The visit function has the following signature:
void (*visitFct)(Node* p, int level, int pos)
Where:
p: pointer to the currently visited nodelevel: the level of visited node| [in] | root | of tree |
| [in] | visitFct | pointer to visit function |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert a node in an extended binary search tree.
insert_by_key_xt(root, p, cmp) inserts the nodepin the extended binary search tree with rootr`.
| [in,out] | r | the tree root |
| [in] | p | the node to insert |
| [in] | cmp | comparison criteria |
p->get_key() is not in the tree, then p is returned (is was inserted). Otherwise it returns Node::NullPtr  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Insert a node in a specific inorder position in a binary tree.
insert_by_pos_xt(r, p, pos) inserts in the position pos the node p.
p, the isnertion could violate the required order for a binary search tree| [in,out] | r | root of tree |
| [in] | p | node to insert |
| [in] | pos | position to insert the node |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert a node in an extended binary search tree without testing for duplicity
| [in,out] | r | the tree root |
| [in] | p | pointer to the node to be inserted |
| [in] | cmp | comparison criteria |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert a node p in a binary search tree
insert_dup_in_bst(root, p) inserts the node p in the binary search tree with root. The key contained in p can be already present in the tree.
| [in,out] | root | of tree |
| [in] | p | pointer to the node to be inserted |
| [in] | cmp | comparison criteria |
p  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert node p as root of a binary search tree. The key of p can be duplicated.
| [in,out] | root | of tree |
| [in] | p | node to insert as root |
| [in] | cmp | comparison criteria |
p which has became the root of tree  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert a node as root of an extended binary search tree.
insert_dup_root_xt(root, p, cmp) inserts the node p as the new root of the tree root.
This insertion allows duplicates.
| [in,out] | root | of tree |
| [in] | p | pointer to the to insert |
| [in] | cmp | comparison criteria |
p that has became root  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Insert a node p in a binary search tree
insert_in_bst(root, p) inserts the node p in the binary search tree with root
| [in,out] | root | of tree. |
| [in] | p | pointer to the node to be inserted. |
| [in] | cmp | comparison criteria. |
p if this was inserted; that is if p->get_key() is not in the tree; otherwise, Node::NullPtr is returned  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Insert a node p as root of an extended binary search tree.
insert_root_xt(root, p) inserts as root in the extended binary search tree root the node p. After insertion, if there is no duplicated key, p becomes the root of the tree.
| [in,out] | root | of tree |
| [in] | p | pointer to the node to insert |
p is not in tree, then returns p, since this was inserted and has became the root. Otherwise, it returns Node::NullPtr  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert the node p as root of a binary search tree
insert_root(root, p, cmp) inserts in the tree root the node p. After insertion, p becomes the new root of tree.
| [in,out] | root | of binary search tree |
| [in] | p | pointer to node to insert |
| [in] | cmp | comparison criteria |
p if this was inserted; that is, if p->get_key() was not present in the tree. Otherwise, no insertion is done and Node::NullPtr is returned  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Insert a node as root in a binary search tree.
This version first insert p as a leaf of tree. Then p is rotated until the root.
| [in] | root | of tree |
| [in] | p | pointer to the node to insert |
| [in] | cmp | comparison criteria |
p if p->get_key() is not in the tree. Otherwise the function returns Node::NullPtr  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Insert a node p as root of an extended binary search tree.
insert_root_xt(root, p) inserts as root in the extended binary search tree root the node p. After insertion, if there is no duplicated key, p becomes the root of the tree.
| [in,out] | root | of tree |
| [in] | p | pointer to the node to insert |
| [in] | cmp | comparison criteria |
p is not in tree, then returns p, since this was inserted and has became the root. Otherwise, it returns Node::NullPtr  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Compute the internal path lenght
| [in] | p | root of tree |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Unión de dos árboles binarios de búsqueda.
join(t,dup) construye un árbol binario de búsqueda correspondiente a la unión de this con t. Las claves duplicadas se inserta, en dup.
| [in] | t | árbol binario de búsqueda que se quiere unir a this. |
| [out] | dup | árbol binario de búsqueda con las claves duplicadas de t. |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Fast union of two binary search trees
join(t1, t2, dup, cmp) joins the nodes of t1 with the nodes of t2. The duplicated keys of t2 are copied in the binary search tree dup.
| [in] | t1 | root of first tree |
| [in] | t2 | root of second tree |
| [out] | dup | tree where the duplicated keys of t2 are put |
| [in] | cmp | comparison criteria |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Unión de dos árboles binarios de búsqueda.
join_dup(t) construye un árbol binario de búsqueda correspondiente a la unión de this con t en la cual pueden haber claves duplicadas.
| [in] | t | árbol binario de búsqueda que se quiere unir a this. |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Exclusive join of two biry trees
join_exclusive(ts, tg) joins ts and ts. The exclusive sense means that all the keys of ts are lesser that all the keys of tg
| [in] | ts | tree with keys lesser than tg |
| [in] | tg | tree with keys greater than ts |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Exclusive union of two extended binary search trees
join_exclusive_xt(ts, tg) joins ts with tg in a tree. The trees must be exclusive in the sense that the all the keys of ts must be lesser than all the keys of tg.
| [in] | ts | extended binary search tree with keys lesser than tg |
| [in] | tg | extended binary search tree with keys greater than tg |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Union of two binary search trees
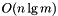 where n and m are the sizes of
where n and m are the sizes of t1 and t2respectively. Use join() which is much more faster| [in] | t1 | root of first tree |
| [in] | t2 | root of second tree |
| [out] | dup | root of tree where the duplicated keys will be put |
| [in] | cmp | comparison criteria |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Return a modifiable reference to the key stored in the node.
|
inline |
Level traverse a tree and execute an operation
operation() must have the following signature:
bool operation(Node* p)
if the result is true then the traversal continues; otherwise it stops.
| [in] | root | of tree |
| [in] | operation | to execute on each visited node |
true if all the nodes were visited; false otherwise  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Traverse a binary tree by levels.
The visit function must have the following signature:
void (*visitFct)(Node* p, int level, bool is_left)
Donde:
p: pointer to currently visited nodepos: ordinal indicating the visit orderis_left: true if p is a left child; false otherwise| [in] | root | of tree |
| [in] | visitFct | visit function |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Return a pointer to left subtree
|
inline |
Load and build a binary tree from a stream
load_tree(input) reads the stream input and load a binary tree previously saved with save_tree().
| [in] | input | stream |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Build a binary tree from two arrays
load_tree_from_array(bits, num_bits, keys) takes a bit array bits of num_bits, whose values of unsigned char type contain the a tree code. The code is therefore read and the tree is built. Afterward, the array keys is read and the values set to the nodes keys in preorder.
The functor Load_Key is used in order to set the node key from a array entry. Its structure must be as follows:
bool load_key(Node * p, const char * str)
The functor must take the string str, perform any needed transformation and set the key of node p. If load_key() returns true then it is assumed that the key was already set and the process advances to the next key. Otherwise, str continues to be the current key and the process advances to the next node. para el siguiente nodo en el recorrido prefijo.
| [in] | bits | array where the tree code is stored |
| [in] | num_bits | number of bits to be read |
| [in] | keys | array where the keys in preorder are stored |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Load the keys stored in preorder from a input stream.
load_tree_keys_in_prefix(root, input) traverses recursively the tree root. For each visited node a key is loaded from the stream
| [in] | root | of tree |
| [in] | input | stream where are the keys in preorder |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Compute the inorder position of a key
| [in] | key | to be searched |
key is not in the tree, then first the first value is -1.
|
inlinenoexcept |
Compute the inorder position of a key
| [in] | r | root of tree |
| [in] | key | to be searched |
key if this is in the tree or -1 if key is not found
|
inline |
Traverse recursively in postorder a binary tree.
postOrderRec(root,visit) performs a inorder traversal of tree rooted by root and on each node exceutes a visit function with the following signature:
void (*visitFct)(Node* p, int level, int pos)
Where:
p: pointer to visted node.level: level of node p.pos: ordinal indicating the visitt order| [in] | root | pointer to tree's root |
| [in] | visitFct | pointer to visit function |
| DynList<Node*> Aleph::prefix | ( | Node * | root | ) |
Return a list with preorder traversal of a tree
| [in] | root | of tree |
| bad_alloc | if there is no enough memory |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
noexcept |
Traverse a tree in preorder via its iterator and performs a conditioned operation on each item.
prefix_traverse(root, operation) instantiates the internal iterator of the class and traverses each item performing operation(p), where p is a node pointer.
operation must have the following signature:
bool operation(Node * p)
If operation(p) returns true then the iterator is advanced and the next item processed. Otherwise. the traversal stops.
| [in] | operation | to be performed on each item |
true if all the nodes were visited (operation on each one always returned true) or false if the traversal was stopped because there was a false result on an item. | anything | that could throw operation |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Build a binary search tree from its preorder traversal
| [in] | preorder | dynamic array where the preorder traversal is found |
| [in] | l | lower index |
| [in] | r | upper index |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Traverse recursively in preorder a binary tree.
preOrderRec(root,visit) performs a inorder traversal of tree rooted by root and on each node exceutes a visit function with the following signature:
void (*visitFct)(Node* p, int level, int pos)
Where:
p: pointer to visted node.level: level of node p.pos: ordinal indicating the visit order| [in] | root | pointer to tree's root |
| [in] | visitFct | pointer to visit function |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Traverse preorder a binary tree without recursion and without stack.
preOrderThreaded(root,visit) traverses preorder the binary tree by building partial threads to succesor nodes. This implicates that during the traversal the links coulld be invalid.
The visit function has the following signature:
void (*visitFct)(Node* p, int level, int pos)
Where:
p: pointer to the currently visited nodelevel: the level of visited node| [in] | root | of tree |
| [in] | visitFct | pointer to visit function |
 Here is the call graph for this function:
Here is the call graph for this function:
|
noexcept |
Return the priority of node
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Remove a key of extended binary tree
remove_by_key_xt(root, key, cmp) searches in the extended binary tree root the key. If key is found, then the node containing it is removed from the tree.
| [in,out] | root | of tree |
| [in] | key | to search and eventually to remove |
| [in] | cmp | comparison criteria |
Node::NullPtr Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Remove from a extended binary tree the node whose inorder position is pos.
| [in,out] | root | of tree |
| [in] | pos | iorder position of node to be removed |
| out_of_range | if pos is greater than the number of nodes of tree |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Remove a key from a binary search tree
| [in,out] | root | of tree |
| [in] | key | to remove |
| [in] | cmp | comparison criteria |
key was found in the tree, Node::NullPtr otherwise Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Return the right tree of p
|
inlinenoexcept |
Rotate to the left the tree with root p
| [in] | p | root to rotate |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Rotate to the left the tree with root p and update its parent
| [in] | p | root to rotate |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Rotate to left the extended bianry tree with root p.
| [in] | p | root to rotate. |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Rotate to the right the tree with root p
| [in] | p | root to rotate |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Rotate to the right the tree with root p and update its parent
| [in] | p | root to rotate |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Rotate to right the extended bianry tree with root p
| [in] | p | root to rotate |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Store a binary tree in a stream
save_tree(root, output) saves the binary tree with root in the stream output. The tree could be restored through load_tree().
The operator << must overloaded for the key of node.
| [in] | root | of tree |
| [out] | output | stream |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Generate C++ array declarations for a binary tree.
save_tree_in_array_of_chars(root, array_name, output) generates two array declarations that would allow to restore the orifinal binary tree. The generated declarations would have the following form:
const unsigned char array_name_cdp[n] = { unsigned char list };
const char * array_name_k[] = { key in prefix order };
The first array is a bit arrat containing the tree code (its Lukasiewicz word). The second array contains a strinficted version of the key values that were generated through the functor Get_Key, whose structure must be as follows:
string get_key(Node * p);
The goodness of this function is to embed binary trees in C++ source code.
| [in] | root | of tree |
| [in] | array_name | prefix name to be added to array variables. |
| [out] | output | stream where the arrays should be written |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Store in output stream the tree keys in preorder
save_tree_keys_in_prefix(root, output) traverses recursively the tree in preorder. For each node, it saves in the stream its key.
Each visit call to functor Get_Key whose function is to extract and return a stringficated version of the key. Its signature must be as follows:
string gk(Node * p)
| [in] | root | of tree |
| [out] | output | stream |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Busca key en arborescencia y calcula el número de Deway del nodo contentivo de la clave key.
search_deway(root,key,deway,n) busca en la arborescencia cuyo primer árbol es root un nodo que contenga la clave key. Si el nodo es encontrado, entonces la rutina guarda en deway[] el número de Deway del nodo encontrado.
La búsqueda se realiza con criterio de igualdad Equal()().
| [in] | root | raÃz del primer árbol de la arborescencia. |
| [in] | key | clave a buscar |
| [out] | deway | arreglo que contiene el número de Deway. |
| [in] | size | tamaño máximo del número de deway. |
| [out] | n | tamaño del número de Deway calculado (si se encuentra el nodo). |
| overflow_error | si size no es suficiente para almacenar la secuencia de Deway. |
|
inlinenoexcept |
Search or insert a node in a binary search tree.
search_or_insert_in_bst(root, p, cmp) searches in root a node containing p->get_key(). If found, then this node is returned. Otherwise p is inserted and returned.
| [in,out] | r | roor of tree |
| [in] | p | node to search or insert |
| [in] | cmp | comparison criteria |
p if its key was not in the tree; otherwise, a pointer containing the tree is returned.  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Search and eventually insert p as root in a binary search tree
| [in] | root | of tree |
| [in] | p | pointer to the node to eventually insert |
| [in] | cmp | comparison criteria |
p is inserted, then it returns p; otherwise, it returns a pointer to the tree node containing to p->get_key()  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Search a key and find its node and parent.
| [in] | root | of tree |
| [in] | key | to search |
| [out] | parent | pointer to parent node if key was found. Otherwise value is undetermined |
| [in] | cmp | comparison criteria |
key if this is found; otherwise, it returns a pointer to the last visited node  Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Rank search of a key in a binary search tree.
In a binary search tree the rank search of a key consists in determining the node that would be parent of key.
search_rank_parent(root, key) searches a node containing key. If key is found, then its node is returned. Otherwise, the last visited node, that would be the parent of key if this was inserted in the tree, is returned.
| [in] | root | of general tree |
| [in] | key | to search |
key if this node exists or the last visited node otherwise
|
inlinenoexcept |
Rank search of a key in a binary search tree.
In a binary search tree the rank search of a key consists in determining the node that would be parent of key.
search_rank_parent(root, key, cmp) searches a node containing key. If key is found, then its node is returned. Otherwise, the last visited node, that would be the parent of key if this was inserted in the tree, is returned.
| [in] | root | of general tree |
| [in] | key | to search |
| [in] | cmp | comparison criteria |
key if this node exists or the last visited node otherwise  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Search a key in a binary search tree
| [in] | root | of tree |
| [in] | key | to search |
| [in] | cmp | key comparison criteria |
Node::NullPtr otherwise  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Iterative selection of a node according to inorder psoition
| [in] | r | root of tree |
| [in] | pos | position inorder whose node wants to be located |
| out_of_range | if pos is greater or equal than the number of nodes. |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Iterative selection of a node according to inorder psoition and determination of parent of selected node
| [in] | r | root of tree |
| [in] | pos | position inorder whose node wants to be located |
| [out] | parent | of selected node |
| out_of_range | if pos is greater or equal than the number of nodes. |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Selecciona un nodo de un árbol binario según su posición infija y lo convierte en su raÃz.
select_gotoup_root(r,i) selecciona el nodo con posición infija i y lo rota hasta que éste devenga su raÃz.
Este algoritmo de selección es recursivo.
| [in] | root | raÃz del árbol binario con rangos. |
| [in] | i | posición infija que se desea acceder. |
| out_of_range | si i es mayor o igual que la cantidad total de nodos del árbol binario. |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Iterative selection of a node according to inorder position without exception.
| [in] | r | root of tree |
| [in] | pos | position inorder whose node wants to be located |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Recursively select the i-th node inorder sense.
| [in] | r | root of tree |
| [in] | i | position inorder sense |
| out_of_range | if i is greater or equal than the number of nodes of overall tree |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Split a binary search tree according to a key.
split_key(root, key, l, r, cmp) splits the tree root according to key. At the end, l contains all the keays lesser than key and r all the keys greater or equal than key.
| [in,out] | root | of tree to split |
| [in] | key | for splitting |
| [out] | l | tree with keys lesser than key |
| [out] | r | tree with keys greater or equal than key |
| [in] | cmp | comparison criteria |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Split a tree according to a key value
split_key_dup_rec(root, key, ts, tg, cmp) splits according to key the tree withrootand build two trees.t1contains the keys lesser thankeyandt2the keys greater or equal thankey`.
| [in,out] | root | of tre to be split |
| [in] | key | for splitting |
| [out] | ts | tree with the keys lesser than key |
| [out] | tg | tree with the keys greater or equal than key |
| [in] | cmp | comparison criteria |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Split an extended binary search tree accoding to a key which can be in the tree.
split_key__dup_rec_xt(root, key, l, r, cmp) splits a tree according a key. The key can be in the tree.
| [in,out] | root | pointer to tree root |
| [in] | key | for splitting |
| [out] | l | tree with keys lesser than key |
| [out] | r | tree with keys greater than key |
| [in] | cmp | comparison criteria |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Split recursively according to a key.
split_key_rec(root, key, ts, tg, cmp) splits the tree with root in two trees t1 which contain the keys lesser than key and t2 which contains the keys greater than key.
The split only is performed if key is not in the tree.
| [in,out] | root | of tree |
| [in] | key | for slitting |
| [out] | ts | tree with keys lesser than key |
| [out] | tg | tree with keys greater than key |
| [in] | cmp | comparison criteria |
true if the tree wa split; that if key was not in the tree. Otherwise the split is not performed and it return false Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Split an extended binary search tree accoding to a key
split_key_rec_xt(root, key, l, r, cmp) splits a tree according a non existing key
| [in,out] | root | pointer to tree root |
| [in] | key | for splitting |
| [out] | l | tree with keys lesser than key |
| [out] | r | tree with keys greater than key |
true if tree was split; that is if key is not in the tree. Otherwise, if key is in the tree, false is returned  Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:
|
inline |
Split a extended binary tree according to a position
split_pos_rec(r, i, ts, tg) splits the tree with root r en two trees ts and tg according to a position i. ts contains the keys from 0 to i - 1 inorder sense and tg the keys from i to n - 1. After completion the original tree r becames empty.
| [in,out] | r | pointer to the root of tree |
| [in] | i | position for splitting |
| [out] | ts | tree where the rank of keys 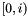 will be put will be put |
| [out] | tg | tree where the rank of keys ![$[i, n]$](form_24.png) will be put will be put |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function:| DynList<Node*> Aleph::suffix | ( | Node * | root | ) |
Return a list with postorder traversal of a tree
| [in] | root | of tree |
| bad_alloc | if there is no enough memory |
 Here is the caller graph for this function:
Here is the caller graph for this function:
|
inlinenoexcept |
Swap a node with its predecessor inorder
| [in] | p | pointer to node to swap with predecessor |
| [in,out] | pp | parent of p |
| [in] | q | predecessor of p |
| [in,out] | pq | parent of q |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inlinenoexcept |
Swap a node with its successor inorder
| [in] | p | pointer to node to swap with successor |
| [in,out] | pp | parent of p |
| [in] | q | successor of p |
| [in,out] | pq | parent of q |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Recorre en sufijo un árbol.
tree_postorder_traversal((root,visit) realiza un recorrido prefijo sobre el árbol con raÃz root. Si visitFct es especificado, entonces, por cada nodo visitado, se invoca la función.
La función de vista tiene la siguiente especificación:
void (visitFct)(Node p, int level, int pos)
Donde:
| [in] | root | raÃz del árbol a visitar. |
| [in] | visitFct | puntero a la función de visita. |
|
inline |
Recorre en prefijo un árbol.
tree_preorder_traversal((root,visit) realiza un recorrido prefijo sobre el árbol con raÃz root. Si visitFct es especificado, entonces, por cada nodo visitado, se invoca la función.
La función de vista tiene la siguiente especificación:
void (visitFct)(Node p, int level, int pos)
Donde:
| [in] | root | raÃz del árbol a visitar. |
| [in] | visitFct | puntero a la función de visita. |
| domain_error | si root no es un nodo raÃz de un árbol. |
|
inline |
Compute a bit code for the binary tree
tree_to_bits(root, array) takes the binary tree with root and computes its prefix code (Lukasiewiczs word) in a bitarray`.
| [in] | root | the root |
| [out] | array | bit array where the code will be stored |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function:
|
inline |
Compute a bit code for the binary tree
tree_to_bits(root) takes the binary tree with root and computes its prefix code (Lukasiewicz`s word) in a bit array
| [in] | root | the root |
| bad_alloc | if there is no enough memory |
 Here is the call graph for this function:
Here is the call graph for this function: Here is the caller graph for this function:
Here is the caller graph for this function: