|
|
void | set_seed (unsigned long seed) noexcept |
| | Set the random number generator seed.
|
| |
|
Compare & | key_comp () noexcept |
| | return the comparison criteria
|
| |
| Compare & | get_compare () noexcept |
| |
| | Gen_Treap_Rk (unsigned long seed, Compare __cmp=Compare()) |
| |
|
| Gen_Treap_Rk (Compare __cmp=Compare()) |
| |
|
void | swap (Gen_Treap_Rk &tree) noexcept |
| | Swap in constant time all the nodes of this with tree
|
| |
|
Node *& | getRoot () noexcept |
| | Return the tree's root.
|
| |
|
Node * | getRoot () const noexcept |
| |
| Node * | search (const Key &key) const noexcept |
| |
| Node * | insert (Node *p) noexcept |
| |
| Node * | insert_dup (Node *p) noexcept |
| |
| Node * | search_or_insert (Node *p) noexcept |
| |
|
bool | verify () const |
| | Return true if the treap is consistent.
|
| |
| Node * | remove (const Key &key) noexcept |
| |
| Node * | remove (const size_t beg, const size_t end) |
| |
| Node * | remove_pos (const size_t pos) |
| |
| Node * | select (const size_t i) const |
| |
|
size_t | size () const noexcept |
| | Return the number of nodes contained in the tree.
|
| |
|
bool | is_empty () const noexcept |
| | Return true if tree is empty.
|
| |
| std::pair< int, Node * > | position (const Key &key) const noexcept |
| |
| std::pair< int, Node * > | find_position (const Key &key) const noexcept |
| |
| bool | split_key (const Key &key, Gen_Treap_Rk &t1, Gen_Treap_Rk &t2) noexcept |
| |
| void | split_key_dup (const Key &key, Gen_Treap_Rk &t1, Gen_Treap_Rk &t2) noexcept |
| |
| void | split_pos (size_t pos, Gen_Treap_Rk &t1, Gen_Treap_Rk &t2) |
| |
| void | join (Gen_Treap_Rk &t, Gen_Treap_Rk &dup) noexcept |
| |
| void | join_dup (Gen_Treap_Rk &t) noexcept |
| |
| void | join_exclusive (Gen_Treap_Rk &t) noexcept |
| |
template<template< class > class NodeType, class Key, class Compare>
class Aleph::Gen_Treap_Rk< NodeType, Key, Compare >
Extended treap (a special type of ramdomized binary search tree) which manages selection and splitting for inorder position.
The treap is a binary search tree whose very high performance is achieved by randomization. The basic idea is to store a priority value in each node which is randomly chosen. By the side of keys, the tree a binary search, but by the side of priorities, the tree is a heap. It is shown that this class of tree has an expected perfomance of  for the majority of its operations. In addition, this extended tree uses and second integer for storing subtrees sizes.
for the majority of its operations. In addition, this extended tree uses and second integer for storing subtrees sizes.
The treap is faster than the randomized tree by a constant time (both approaches are logarithmic). Since the priority is chosen just one time and the adjustements are done in a botton-top way (by contrast with the randomized which is top-bottom), the treap takes less time.
Although tgus approach trends to be faster than the randomized trees, takes in account that this treap is more space consuming because each node requires 2 additional integers to the data (priority and counter) in constrast with the radomized which only requieres one interger (the counter).
For splitting and join of independent and large data sets the ramdomized option trends to be faster. The split is equivalent, but the join is definitively faster. The join of two trees of n and m keys respectively takes 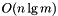 with treaps, while it takes
with treaps, while it takes 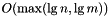 with radomized trees. In addition,
with radomized trees. In addition,
The class internally uses the gsl random number generator of GSL - GNU Scientific Library. By default, the Mersene twister is used and the seed is taken from system time.
- See also
- Treap Treap_Vtl Treap_Rk Treap_Rk_Vtl Rand_Tree
template<template< class > class NodeType, class Key, class Compare>
| std::pair<int, Node*> Aleph::Gen_Treap_Rk< NodeType, Key, Compare >::find_position |
( |
const Key & |
key | ) |
const |
|
inlinenoexcept |
Find the inorder position of a key in the tree.
find_position(key) determines the inorder position that has or had key in the tree. Themethod return a tuple with a position and a node pointer.
If key is found then its inorder position is returned along with a pointer to the node containing it.
Otherwise, the the tuple returns the position that would have key if this was in the tree and the parent node that the key would had. At this regard, there are three cases:
- if
key is lesser than the minimum key of tree, then first is -1 and the node is one with the smallest key.
- If
key is greater than the maximum key in the tree, then first is the number of keys and the node is one with the maximum key in the tree.
- For any other case, first is the inorder position that would have
key if this was in the tree and second is the node whose key is inmediataly greater than key.
- Parameters
-
- Returns
- a pair with the inorder position and and related node
 for the majority of its operations. In addition, this extended tree uses and second integer for storing subtrees sizes.
for the majority of its operations. In addition, this extended tree uses and second integer for storing subtrees sizes.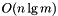 with treaps, while it takes
with treaps, while it takes 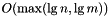 with radomized trees. In addition,
with radomized trees. In addition, Here is the caller graph for this function:
Here is the caller graph for this function: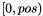 will be put
will be put ![$[pos, n]$](form_41.png) will be put
will be put