#include <tpl_binTree.H>

Classes
struct	Iterator

Public Types
using	Node = NodeType< Key >

Public Member Functions
	GenBinTree (const GenBinTree &)=delete

GenBinTree &	operator= (const GenBinTree &)=delete

void	swap (GenBinTree &tree) noexcept
	Swap `this` with `tree` in constant time.

Compare &	key_comp () noexcept
	return the comparison criteria

Compare &	get_compare () noexcept

	GenBinTree (Compare __cmp=Compare()) noexcept
	Initialize an empty tree with comparison criteria `__cmp`

Node *	search (const Key &key) const noexcept

bool	verify () const
	Return `true` if the tree is a consistent (correct) binary search tree.

Node *&	getRoot ()
	Return the root of tree.

bool	verifyBin () const

Node *	insert (Node *p) noexcept

Node *	insert_dup (Node *p) noexcept

Node *	search_or_insert (Node *p) noexcept

bool	split (const Key &key, GenBinTree &l, GenBinTree &r) noexcept

void	split_dup (const Key &key, GenBinTree &l, GenBinTree &r) noexcept

Node *	remove (const Key &key) noexcept

void	join (GenBinTree &tree, GenBinTree &dup) noexcept

void	join_dup (GenBinTree &t) noexcept

void	join_exclusive (GenBinTree &t) noexcept

Detailed Description

template<template< typename > class NodeType, typename Key, class Compare>
class Aleph::GenBinTree< NodeType, Key, Compare >

Simple binary search tree.

This class implements a simple binary search tree. By simple we want to say that no balance operation are done. Consequently the performance depends on whether keys insertion order.

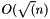In general, if the insertion order is random and there is no many removals, the this tree is very good and its operations trend to be $O(\lg n)$ . If there are many removals, the performance is lightly degraded trending to be $O(\sqrt(n)$ .

If you cannot assure that the insertion order is random, then do not use this tree.

See also: BinTree BinTreeVtl DynBinTree

Member Function Documentation

◆ get_compare()

template<template< typename > class NodeType, typename Key, class Compare>

Compare& Aleph::GenBinTree< NodeType, Key, Compare >::get_compare ( )

inlinenoexcept

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

◆ insert()

template<template< typename > class NodeType, typename Key, class Compare>

Node* Aleph::GenBinTree< NodeType, Key, Compare >::insert ( Node * p )

inlinenoexcept

Insert a node in the tree

Parameters

[in] p pointer to the node to insert

Returns: if p->get_key() is not in the tree, then the pointer p is returned (it was inserted); othewise, nullptr is returned

Here is the caller graph for this function:

◆ insert_dup()

template<template< typename > class NodeType, typename Key, class Compare>

Node* Aleph::GenBinTree< NodeType, Key, Compare >::insert_dup ( Node * p )

inlinenoexcept

Insert a node in the tree.

This method does not fail. It always inserts.

Parameters

[in] p pointer to the node to insert

Returns: the p pointer

Here is the caller graph for this function:

◆ join()

template<template< typename > class NodeType, typename Key, class Compare>

void Aleph::GenBinTree< NodeType, Key, Compare >::join	(	GenBinTree< NodeType, Key, Compare > &	tree,
		GenBinTree< NodeType, Key, Compare > &	dup
	)

inlinenoexcept

Join tree with this. Duplicated keys of tree are put in dup parameter.

Parameters

[in,out]	tree	to join with `this`
[out]	dup	tree where the duplicated key belonging to `tree` are put.

Here is the caller graph for this function:

◆ join_dup()

template<template< typename > class NodeType, typename Key, class Compare>

void Aleph::GenBinTree< NodeType, Key, Compare >::join_dup ( GenBinTree< NodeType, Key, Compare > & t )

inlinenoexcept

Join this with t independently of the presence of duplicated keys

join(t) produces a random tree result of join of this and t. The resulting tree is stored in this.

Parameters

[in] t tree to join with this keys are inserted

Here is the caller graph for this function:

◆ join_exclusive()

template<template< typename > class NodeType, typename Key, class Compare>

void Aleph::GenBinTree< NodeType, Key, Compare >::join_exclusive ( GenBinTree< NodeType, Key, Compare > & t )

inlinenoexcept

Join exclusive of this with t

Exclusive means that all the keys of this are lesser than all the keys of t. This knowlege allows a more effcient way for joining that when the keys ranks are overlapped. However, use very carefully because the algorithm does not perform any check and the result would be incorrect.

Parameters

[in] t tree to exclusively join with this keys are inserted

Here is the caller graph for this function:

◆ remove()

template<template< typename > class NodeType, typename Key, class Compare>

Node* Aleph::GenBinTree< NodeType, Key, Compare >::remove ( const Key & key )

inlinenoexcept

Remove a key from the tree

Parameters

[in] key to remove

Returns: a valid pointer to the removed node if key was found in the tree, nullptr otherwise

◆ search()

template<template< typename > class NodeType, typename Key, class Compare>

Node* Aleph::GenBinTree< NodeType, Key, Compare >::search ( const Key & key ) const

inlinenoexcept

Search a key.

Parameters

[in] key to be searched

Returns: a pointer to the containing key if this was found; otherwise nullptr

Here is the caller graph for this function:

◆ search_or_insert()

template<template< typename > class NodeType, typename Key, class Compare>

Node* Aleph::GenBinTree< NodeType, Key, Compare >::search_or_insert ( Node * p )

inlinenoexcept

Search or insert a key.

search_or_insert(p) searches in the tree the key KEY(p). If this key is found, then a pointer to the node containing it is returned. Otherwise, p is inserted.

Parameters

[in] p node containing a key to be searched and eventually inserted

Returns: if the key contained in p is found, then a pointer to the containing key in the tree is returned. Otherwise, p is inserted and returned

Here is the caller graph for this function:

◆ split()

template<template< typename > class NodeType, typename Key, class Compare>

bool Aleph::GenBinTree< NodeType, Key, Compare >::split	(	const Key &	key,
		GenBinTree< NodeType, Key, Compare > &	l,
		GenBinTree< NodeType, Key, Compare > &	r
	)

inlinenoexcept

Split the tree according to a key

split(key, l, r) splits the tree according to key. That is, if key is not present in the tree, then the tree is split in two trees l which contains the key lesser than key and r which contains the keys greater than key. If key is found in the tree, then the split is not done

Parameters

[in]	key	for splitting
[out]	l	resulting tree with the keys lesser than `key`
[out]	r	resulting tree with the keys greater than `key`

Returns: true if the tree was split. false otherwise

◆ split_dup()

template<template< typename > class NodeType, typename Key, class Compare>

void Aleph::GenBinTree< NodeType, Key, Compare >::split_dup	(	const Key &	key,
		GenBinTree< NodeType, Key, Compare > &	l,
		GenBinTree< NodeType, Key, Compare > &	r
	)

inlinenoexcept

Split the tree according to a key that could be in the tree

split_dup(key, l, r) splits the tree according to key in two trees l which contains the key lesser than key and r which contains the keys greater or equal than key.

Parameters

[in]	key	for splitting
[out]	l	resulting tree with the keys lesser than `key`
[out]	r	resulting tree with the keys greater or equal than `key`

◆ verifyBin()

template<template< typename > class NodeType, typename Key, class Compare>

bool Aleph::GenBinTree< NodeType, Key, Compare >::verifyBin ( ) const

inline

This is an overloaded member function, provided for convenience. It differs from the above function only in what argument(s) it accepts.

The documentation for this class was generated from the following file:

tpl_binTree.H

Classes

Public Types

Public Member Functions

Detailed Description

template<template< typename > class NodeType, typename Key, class Compare> class Aleph::GenBinTree< NodeType, Key, Compare >

Member Function Documentation

◆ get_compare()

◆ insert()

◆ insert_dup()

◆ join()

◆ join_dup()

◆ join_exclusive()

◆ remove()

◆ search()

◆ search_or_insert()

◆ split()

◆ split_dup()

◆ verifyBin()

template<template< typename > class NodeType, typename Key, class Compare>
class Aleph::GenBinTree< NodeType, Key, Compare >