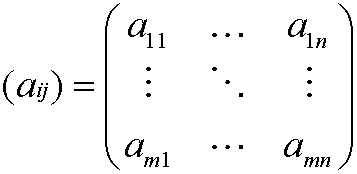Álgebra Lineal

Problemas del curso Álgebra 1
Semestre B 2005 - Facultad de Humanidades- Escuela de Educación.

Contenido:

Evaluaciones.

Capítulo 1. Cuerpo y espacios vectoriales.

Capítulo 2. Matrices.

Capítulo 3. Aplicaciones Lineales.

Capítulo 4. Producto escalar.

¿ Qué es una variedad lineal?

La matriz del Constructor

Capítulo 5. Determinantes

 

Capítulo 1.

Cuerpos

  1. Sea  A = { a, b , c}. ¿ Cuáles de las siguientes operaciones sobre A son operaciones binarias? Indique cuáles son asociativas, conmutativas. Determine si hay elemento neutro en cada uno de los casos. Construya tablas para éstas operaciones. Busque el inverso de cada elemento.    a $ b =  a.,  a* b = c.
  2.  Probar que si K es un cuerpo, entonces 0.a = 0 , para todo a en K.
  3. Probar que si K es un cuerpo, entonces el elemento neutro para la suma,0,  es único.

 Espacios vectoriales

  1. Probar que el conjunto de los números reales es un espacio vectorial sobre Q.
  2. Probar que R3 , el conjunto de tripletas ordenadas de números reales de la forma ( x, y, z) es un espacio vectorial sobre R, con la suma y producto por un escalar definidas de la siguiente forma :

        Suma : 

( x 1 ,y 1 , z 1 ) + ( x 2 ,y 2 , z 2 )  = ( x 1 +   x 2 , y 1 +   y 2    ,  z 1 +   z 2  )

       Producto por un escalar: 

a · ( x, y, z) = ( a x, a y, a z).

 3. Generalización del ejercicio anterior. Sea R n   , el conjunto de n-uplas ordenadas de números reales de la forma ( x 1 ,x 2 , ...., x n ) . Definimos en este conjunto una suma y multiplicación por un escalar dadas por

Suma:

( x 1 ,x 2 , ...., x n ) + ( y 1 , y 2 , ...., y n ) = ( x 1 +   y 1 , x 2 +   y 2  ,....,  x n +   y n  )

Producto por un escalar: 

a ·  ( x 1 ,x 2 , ...., x n ) =  ( a x 1 ,a x 2 , ...., a x n ).

Demuestre que  R n  con estas operaciones es un espacio vectorial.

4. Sea  R [x] el conjunto de los polinomios con coeficientes reales cuyos elementos son de la forma

p (x) =  a0  +   a1 x  +  a2 x 2  + .....+  a n x n    ,

donde a0 ,   a1 ,  .....,  a n    son números reales.   

Demuestre que   R [x]   , es un espacio vectorial con las operaciones

Suma de polinomios:

p( x) + q( x) =  a0 +  b0   +   ( a1  +  b1   )  x  +   ( a2  +  b2   ) x 2  + .....+   ( a n  +  b n   ) x n    ,

Producto de un número real por un polinomio:

a · p( x) =  a · (    a0  +   a1 x  +  a2 x 2  + .....+  a n x n   ) =   a  a0  +   a a1 x  +  a a2 x 2  + .....+ a  a n x n   

5. Sea M 2x2( R) el conjunto de las matrices 2x2 con entradas reales, cuyos elementos son de la forma:

 

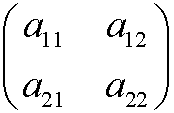
  donde los a  i j , son números reales.

Demuestre que M 2x2( R) es un espacio vectorial con las operaciones:

Suma de matrices:

producto de un número real por una matriz:

 

6. Sea M n x m( R) el conjunto de las matrices de n filas y m columnas a valores reales , cuyos elementos son de la forma

con las operaciones de suma y producto por un escalar dadas por

Probar que M n x m( R)  es un espacio vectorial.

 

7. Sea  B([0, 1]) el conjunto  de las funciones reales acotadas definidas en el intervalo cerrado [ 0, 1]. Demuestre que este conjunto es un espacio vectorial con las operaciones dadas :

Suma de funciones:

(f + g) (x) = f( x) + g( x) , para todo x en [ 0, 1]

Producto de un número real por una función

(c. f) (x) = c · f( x), para todo x en [ 0, 1] .

8. Sea C el conjunto de los números complejos, cuyos elementos son de la forma a + b i . con a y b números reales e i es un símbolo tal que  i 2 = -1. Probar que C es un espacio vectorial sobre R.

 

          Subespacios

      1. Sea W el subconjunto de R2 , definido por W = { ( x, y) / x = 2y }. Probar que W es un subespacio de R2.

        2. Sea U el subconjunto del plano cuyos elementos ( x, y) satisfacen x2  = y. Probar que U no es un subespacio de R2.

        3. Sea H el conjunto de todos los polinomios de grado menor o igual a tres. ¿ Es H un subespacio del espacio vectorial de los polinomios con coeficientes reales R [x] ? En caso afirmativo dar una justificación.

        4. Sea M(Q) el conjunto de las matrices 2x2 con coeficientes racionales. Determinar si M (Q) es un subespacio del espacio vectorial M2x2( R).

        5. Sea D 2x2( R), el conjunto de matrices diagonales 2x2, cuyos elementos situados fuera de la diagonal son todos iguales a cero. Demuestre que  D 2x2( R) , es un subespacio de M2x2( R).

        6. Sea S el conjunto de números complejos z, que satisfacen   | z |≤ 2 . ¿ Es S un subespacio de los números complejos C?

 

    Combinaciones lineales.

 

        1. Exprese el vector   v = ( 1, 2 ) como una combinación lineal de los vectores u = ( -1, 0) y w = ( 3, 3 ).

        2. Exprese el vector   v = ( 1, 1, -4 ) como una combinación lineal de los vectores u = ( 5, 0, 1) ,  w = ( 3, 3 , 2) y z = ( 0, 2, 4 )

        3. Determine si el polinomio p( x) = 5 x2  + x - 1. se puede escribir como combinación lineal de los polinomios q( x) =   x2  + x , y 

            s( x)   =  x2  + x  -2.

        4. Una matriz elemental cuadrada de orden 3, denotada por E ij , es aquella que tiene un uno en la posición i j y 0 en las restantes. Demuestre que toda matriz cuadrada de orden tres es combinación lineal de matrices elementales.

        5. Demuestre que todo polinomio de grado menor o igual a dos es combinación de los polinomios:  x2   , x-1 y x +1.

        6. Hallar números reales a y b  , tales que

            a ( 1, 2) + b ( 1, -5 ) = ( 0, 0).

        7. Hallar números reales a, b, y c tales que

        a v1  +   b v2   +   c v3  = 0.

        donde  v1  = ( 2, -3, -3),  v2  = ( 0, 1, -3) y  v3  = ( 2, 0, 1).

 

Dependencia lineal, bases, dimensión

 

    1)Determinar si los vectores u = ( 1, -2, 1) , v = ( 2, 1, -1) , w = ( 7, -4, 1) son linealmente dependientes.

    2) Sea v = ( 1, 2, -3 ) , w = ( 1, 0, 5 ) y  u = ( 1, 1, 1 ) . Determinar si estos vectores forman una base de  R3 .

    3) Halle una base para el espacio de todos los polinomios con coeficientes reales de grado menor o igual a tres.

    4) Sea s = ( 1, 0, 3, 0 ) y  v = ( 1, -1, -1, 4 ) . Hallar dos vectores de  R4 ,   u y w , tales que B = { s, v, u, w } sea una base del espacio.

    5) Halle la dimensión del espacio formado por las matrices cuadradas de orden 3 x 3 diagonales.

    6) Encontrara un subconjunto de  u 1,  u 2,  u 3,  u 4  que sea base de la envolvente lineal:   lin (   u 1,  u 2,  u 3,  u 4   ) de R , donde 

    a)  u 1 = ( 1, 1, 1, 2, 3 ) , u 2 = ( 1, 2, -1, -2, 1 ) ,  u 3 = ( 3, 5, -1, -2, 5 ) , u 4 = ( 1, 2, 1, -1, 4 ) ,

    b) u 1 = ( 1, -2, 1, 3, -1 ) , u 2 = ( -2, 4, -2, -6, 2 ) ,  u 3 = ( 1, -3, 1, 2, 1 ) , u 4 = ( 3, -7, 3, 8, -1 )  .

 

Sumas y Sumas directas.

    1) Considérense los siguientes subespacios de R4 ,

    U = lin { (1, 1, 0, -1 ), ( 1, 2, 3, 0) , ( 2, 3, 3, 0) }.

    W = lin { (1, 2, 2, -2), ( 2, 3, 2, -3), ( 1, 3, 4, -3) }

Hallar: a) dim ( U + W), b) dim ( U ⋂ W ).

    2) Sean U y W los siguientes subespacios de  R4 ,  U = { ( a, b, c, d) / b + c + d = 0 }, W = { ( a, b, c, d) / a + b = 0, c = 2d }.

Encontrar una base y la dimensión de a ) U,  b) W, c ) U ⋂ W d ) U + W.

    3) Demuestre que R , es igual a la suma directa de los vectores v = ( 1, 1, 1) v = ( 1, 2, 0 ) y w = ( 0, 0, 2) .